The Perceptron Algorithm and the Kernel Trick

The Perceptron Algorithm is one of the earliest and most influential machine learning models, forming the foundation for modern neural networks and support vector machines (SVMs). Proposed by Frank Rosenblatt in 1958 (Rosenblatt, 1958), the perceptron is a simple yet powerful linear classifier designed for binary classification tasks. 

Despite its simplicity, the perceptron introduced key concepts that remain central to machine learning today, such as iterative weight updates, the use of activation functions, and learning a decision boundary (Goodfellow, Bengio & Courville, 2016). These ideas have directly influenced the development of multi-layer neural networks by introducing weight adjustment rules that underpin backpropagation (LeCun, Bengio & Hinton, 2015). 

The perceptron's weight update mechanism, based on error correction, serves as an early precursor to the gradient-based optimization used in modern deep learning (Rumelhart, Hinton & Williams, 1986). However, its limitations in handling non-linearly separable data led to the development of advanced techniques like the Kernel Trick, which extends the perceptron's capabilities to more complex datasets (Schölkopf & Smola, 2002).

The Perceptron Algorithm

The perceptron operates by learning a hyperplane that separates two classes in a dataset. Given a set of input features and corresponding labels, the algorithm initializes weights and iteratively updates them based on classification errors. The goal is to find a hyperplane that correctly classifies all training instances, assuming the data is linearly separable.

Algorithm

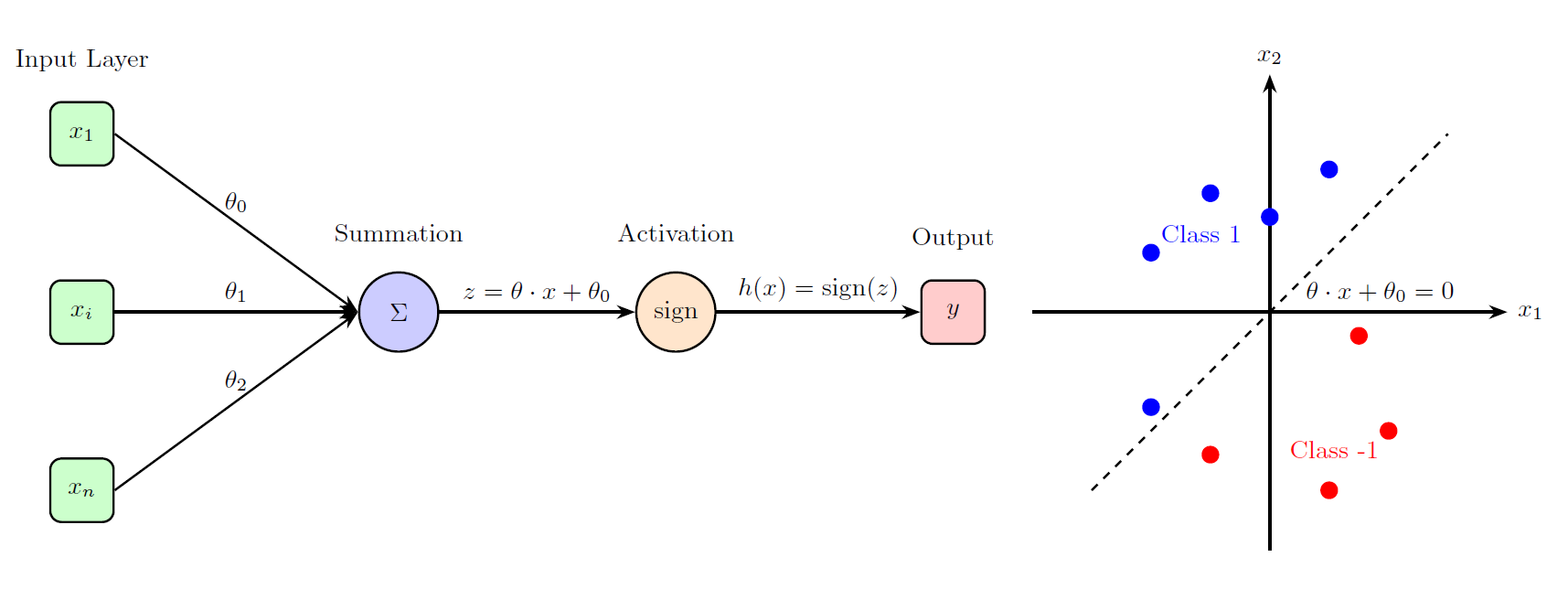
Limitations of the Perceptron

While the perceptron is effective for linearly separable data, it has significant limitations:

• Linear separability. The perceptron can only classify data that is linearly separable. If no hyperplane can perfectly separate the two classes, the algorithm will fail to converge and will continue updating weights indefinitely (Minsky & Papert, 1969).
• Noisy data. The perceptron is sensitive to noise and outliers, which can prevent convergence even if the data is mostly separable.
• Lack of probabilistic output. The perceptron provides a hard decision boundary without any measure of confidence or probability.

The Kernel Trick: Extending the Perceptron

To handle non-linearly separable data, one approach is to map the input into a higher-dimensional space where it becomes linearly separable. For example, a 2D input space can be transformed into a 3D space using non-linear mapping, making linear separation possible. However, such transformations can be computationally expensive — if the input has DDD features, a polynomial transformation of degree p can lead to O(d^p) features. This exponential growth quickly becomes infeasible for large datasets.

To overcome this limitation, Aizerman et al. (1964) introduced the Kernel Trick. This technique enables models like the perceptron and support vector machines (SVMs) to operate in a high-dimensional space without explicitly computing the transformation, significantly reducing computational complexity.

Instead of computing the transformed features explicitly, the Kernel Trick computes the inner product of two transformed feature vectors directly using a kernel function:

                                                                    K(x, x') = φ (x) .φ (x')

This avoids the need for explicit transformation while still benefiting from the higher-dimensional representation.  

Common Kernel Functions  

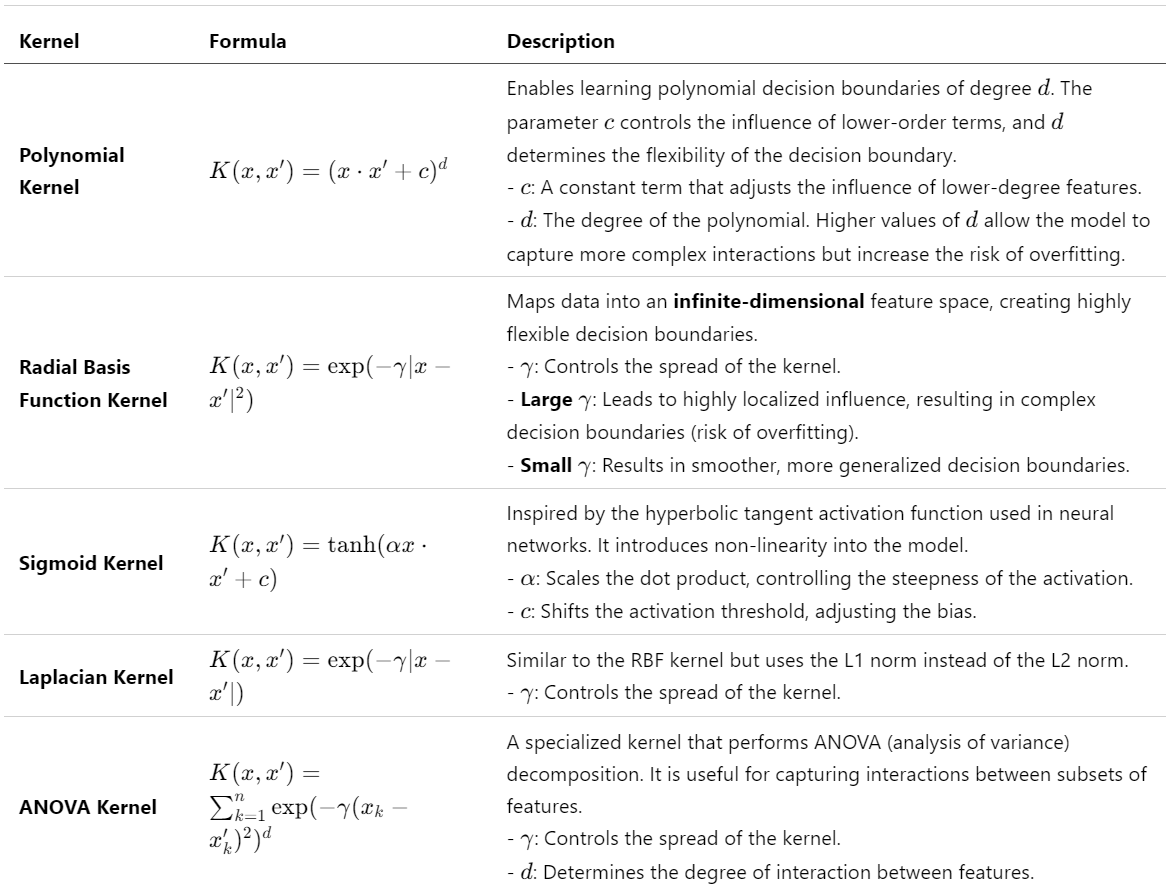
Kernelized Perceptron  

The classical perceptron algorithm relies on dot products to update weights. In a kernelized perceptron, we replace all dot products with kernel evaluations, allowing the perceptron to operate in an implicit higher-dimensional space.

This formulation means the perceptron does not need explicit feature mappings, making it computationally efficient while still benefiting from high-dimensional representations.

Advantages of the Kernel Trick

• Non-linear decision boundaries. The kernel trick enables the perceptron to learn complex, non-linear decision boundaries.
• Computational efficiency. By avoiding explicit computation of higher dimensions, the kernel trick reduces computational complexity.
• Versatility. The choice of kernel function significantly impacts model performance. Different kernels capture different types of relationships in the data. Polynomial kernels are effective for capturing interactions between features, while RBF kernels are well-suited for complex, high-dimensional datasets. The sigmoid kernel is sometimes used as a proxy for neural network architectures. Selecting an appropriate kernel is crucial as it affects both the accuracy and computational efficiency of the model (Scholkopf & Smola, 2002).

Implementation and Practical Considerations

The kernelized perceptron is often implemented as part of larger machine learning frameworks. Libraries such as Scikit-learn and TensorFlow provide implementations of kernelized models, making it easier to experiment with different kernel functions and optimize performance for real-world datasets. 

Additionally, feature selection plays a critical role when applying kernel methods. Choosing an appropriate kernel and tuning its hyperparameters significantly affect the accuracy and generalizability of the model. Hyperparameter optimization techniques, such as grid search or Bayesian optimization, are often employed to improve model performance.

Conclusion

The Perceptron Algorithm represents a cornerstone in the evolution of machine learning. Introducing fundamental concepts such as iterative weight updates, activation functions, and linear decision boundaries laid the groundwork for modern techniques like neural networks and support vector machines. 

While its simplicity and effectiveness in linearly separable tasks were groundbreaking, the perceptron's inability to handle non-linear data highlighted its limitations. This challenge spurred the development of advanced methods, most notably the Kernel Trick, which enabled the creation of non-linear decision boundaries without explicit high-dimensional computations. 

These innovations extended the perceptron's applicability and paved the way for more sophisticated models like SVMs and deep neural networks. Today, the principles introduced by the perception — such as error correction and gradient-based optimization — remain central to machine learning, underscoring its enduring influence on the field. The perceptron's legacy is a testament to the importance of foundational ideas in driving the continuous advancement of artificial intelligence.

References

• Rosenblatt, F. (1958). The Perceptron: A Probabilistic Model for Information Storage and Organization in the Brain. Psychological Review, 65(6), 386–408.
• Goodfellow, I., Bengio, Y., and Courville, A. (2016). Deep Learning. MIT Press.
• LeCun, Y., Bengio, Y., and Hinton, G. (2015). Deep Learning. Nature, 521(7553), 436–444.
• Rumelhart, D. E., Hinton, G. E., and Williams, R. J. (1986). Learning Representations by Back-Propagating Errors. Nature, 323(6088), 533–536.
• Scholkopf, B., and Smola, A. J. (2002). Learning with Kernels: Support Vector Machines, Regularization, Optimization, and Beyond. MIT Press.