Handling Vectors in AI Context via PostgreSQL pgVector
An introduction to PostgreSQL pgVector extension and its supported metrics — L2 squared distance (Euclidian), dot product, cosine distance/similarity.
Join the DZone community and get the full member experience.
Join For FreeRelational databases are optimized for storing and querying structured data, yet most of the data today is unstructured. Artificial Intelligence and Machine Learning are now able to “structure” pieces of unstructured data without altering its semantics. First, they transform it ‘conveniently’ into arrays of numbers, structures that are called vectors. Then, the vectors are stored in dedicated databases and worked upon as needed, so that the initial data becomes useful and meaningful as part of a high-dimensional space.
In the context of AI, the numerical arrays are called vector embeddings and can be seen as sets of “characteristics” of the represented entities (objects). Their role is to allow AI models to infer from them and consequently on the initial input data.
This article is an introduction to how to turn PostgreSQL into a vector database using the pgVector extension. It also briefly presents a few general vector similarity concepts, concepts that are relevant, particularly in AI applications.
Concepts
As developers become more and more interested in constructing AI functionalities (or exploring them), it is useful and helpful to have a basic understanding of the concepts around vectors in a multi-dimensional space. Moreover, when using techniques such as Retrieval Augmentation Generation (RAG) where vector embeddings enrich the AI context to fulfill the user’s inquiries, this basic understanding becomes a prerequisite.
In general, Large Language Models (LLMs) are stateless, and it isn’t seldom when the responses they give to prompts are not satisfactory. In order to enhance their capabilities, they are improved with “state” represented as vector embeddings. It is said that this state is used to provide LLMs with “a long-term memory” so that the possibility of them hallucinating decreases. Basically, when a prompt is provided to a model, in case the results are not satisfactory, one may “help” it with relevant pieces of information – embeddings – extracted from the self-vector databases.
To accomplish this, at least two preconditions are needed:
- Gather the data, transform it into vector embeddings, and have it stored in the database
- When needed, quickly find the vectors related to the ones in the prompt and “hand” it to the model to use it
The former step represents the “magical” operation through which an ML model accepts text as input and through vectorization, transforms it into vectors. The latter is accomplished by leveraging the features offered by the chosen vector database.
When it comes to vector databases, there are quite a bunch of implementations available. A few are mentioned below:
- PostgreSQL pgVector – in this article
- AzureVector
- ChromaVector
- MilvusVector
- Neo4jVector
- PineconeVector
- QdrantVector
- RedisVector
- WeaviateVector
According to OpenAI, “the distance between two vectors measures their relatedness. Small distances suggest high relatedness and large distances suggest low relatedness.”
With this definition in mind, it is said that the similarity of two objects is the distance between their vector representations using a specific metric (method).
The “theory” defines several such metrics:
- L1 distance (Manhattan)
- L2 squared distance (Euclidian)
- dot product
- cosine distance/similarity
- Hamming distance
Choosing a certain metric depends on several factors, yet this aspect won’t be detailed as part of this article. Nevertheless, as the pgVector extension currently supports L2, dot product, and cosine distance/similarity metrics, these are the ones analyzed next.
Installing pgVector
As of now, PostgreSQL does not support vector similarity search natively. In order to accommodate such a feature, the pgVector extension may be added. According to the documentation, one needs to perform a few simple steps [Resource 1].
Personally, I used an existing PostgreSQL 13.11 server running on Windows OS and I enhanced it with vector support by compiling, installing, and enabling the extension afterward.
Steps:
- Install Visual Studio 2022 with C++ support, available here
- Run
vcvars64.bat, located inMicrosoft Visual Studio\2022\Community\VC\Auxiliary\Build\directory - Set
PGROOTto point to the current PostgreSQL
>set "PGROOT=C:\Program Files\PostgreSQL13"- Get the
pgVectorsource code
>git clone --branch v0.6.2 https://github.com/pgvector/pgvector.git- Go to the
pgvectordirectory and run the make file using usingnmake
>nmake /F Makefile.win
>nmake /F Makefile.win install- Enable the extension using the next SQL command
create extension vector;At this point, one shall be able to use a new data type in their tables – vector, store data as vectors, and perform similarity search queries.
Querying Vectors in PostgreSQL
The way a Machine Learning model transforms the text into vectors (“the magic”) is not considered as part of this article. Thus, it is assumed that the vector embeddings exist, and they are ready to be stored in the database.
Let the following three sentences have the following representations. For convenience, a space with three dimensions is used.
'Raccoons are silly and funny.' - [3,0,4]
'Dogs are friendly and helpful.' - [5,0,2]
'Cats are funny and foxy.' - [4,0,3]Since the vectors are available, they can be stored. Prior to that, a new schema and a minimal table are created.
create schema vectors;
create table if not exists document (
id integer primary key,
name text not null,
content text not null,
embedding vector(3) not null
);One may notice that the fourth column – embedding – and its vector data type. The parameter represents the number of dimensions, here 3.
insert into document
values (1, 'Raccoons', 'Raccoons are silly and funny.', '[3,0,4]');
insert into document
values (2, 'Dogs', 'Dogs are friendly and helpful.', '[5,0,2]');
insert into document
values (3, 'Cats', 'Cats are funny and foxy.', '[4,0,3]');The data is in, one may start launching queries.
select * from document;+--+--------+------------------------------+---------+
|id|name |content |embedding|
+--+--------+------------------------------+---------+
|1 |Raccoons|Raccoons are silly and funny. |[3,0,4] |
|2 |Dogs |Dogs are friendly and helpful.|[5,0,2] |
|3 |Cats |Cats are funny and foxy. |[4,0,3] |
+--+--------+------------------------------+---------+Metrics
Next, each of the metrics pgVector currently supported is analyzed. The context is simple.
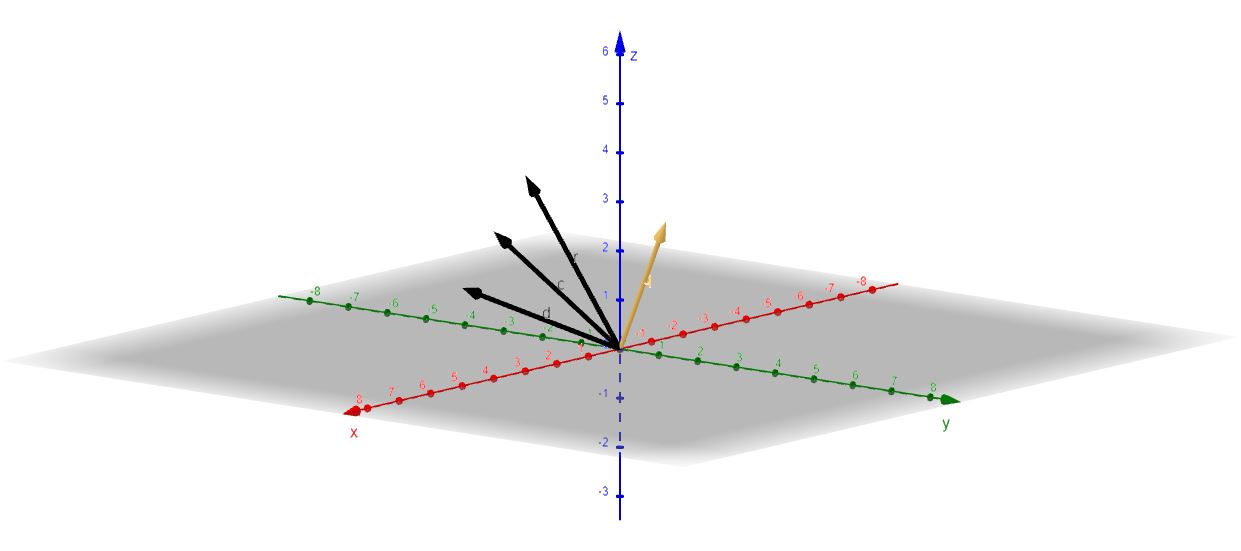
Let’s consider, in addition to the three vector embeddings, a fourth one – [1,2,3]. As the focus is not on how a vector is produced, we could say it may mean anything. The aim is to find out how similar the stored vectors are to this one.
Graphically, the four vectors can be represented as below.
L2
L2 (Euclidian) squared distance between two vectors represents the straight-line distance between them.
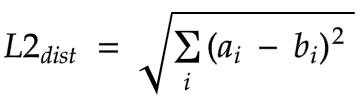
The lower the distance, the more similar the vectors.
E.g. the L2 distance between [3,0,4] (“Raccoons are silly and funny.”) and [1,2,3] (our query) is
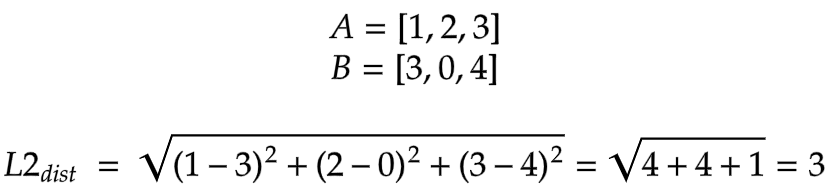
In PostgreSQL, the <-> operator computes the L2 distance.
select *, embedding <-> '[1,2,3]' as l2_distance
from document
order by l2_distance;+--+--------+------------------------------+---------+-----------------+
|id|name |content |embedding|l2_distance |
+--+--------+------------------------------+---------+-----------------+
|1 |Raccoons|Raccoons are silly and funny. |[3,0,4] |3 |
|3 |Cats |Cats are funny and foxy. |[4,0,3] |3.605551275463989|
|2 |Dogs |Dogs are friendly and helpful.|[5,0,2] |4.58257569495584 |
+--+--------+------------------------------+---------+-----------------+Dot Product
The dot product of two vectors is nothing but the scalar product between the two. The dot product distance between the vectors is the negative of their dot product.
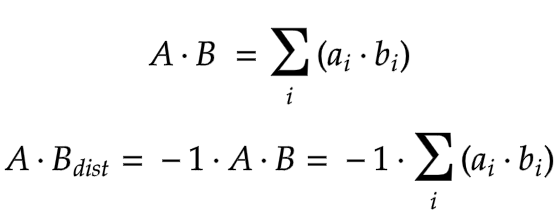
The lower the distance, the more similar the vectors.
E.g. the dot product distance between [3,0,4] (“Raccoons are silly and funny.”) and [1,2,3] (our query) is:
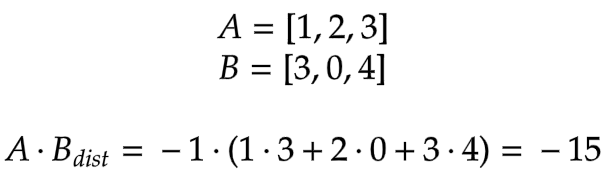
In PostgreSQL, the <#> operator computes the dot product distance.
select *, embedding <#> '[1,2,3]' as dp_distance
from document
order by dp_distance;+--+--------+------------------------------+---------+-----------+
|id|name |content |embedding|dp_distance|
+--+--------+------------------------------+---------+-----------+
|1 |Raccoons|Raccoons are silly and funny. |[3,0,4] |-15 |
|3 |Cats |Cats are funny and foxy. |[4,0,3] |-13 |
|2 |Dogs |Dogs are friendly and helpful.|[5,0,2] |-11 |
+--+--------+------------------------------+---------+-----------+Cosine Similarity / Distance
The cosine similarity between two vectors is the cosine of the angle between the two in the considered space.
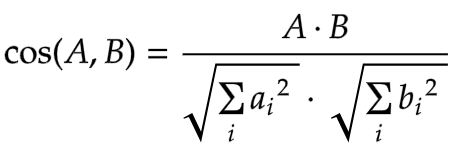
The smaller the angle, the more similar the vectors. Also, it is said that similar vectors point towards the same direction.
The cosine distance is defined as the “complementary” of the cosine similarity.
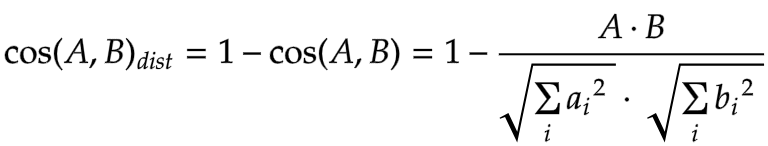
The lower the distance (the bigger the cosine similarity), the more similar the vectors.
e.g. the cosine similarity and the cosine distance between [3,0,4] (“Raccoons are silly and funny.”) and [1,2,3] (our query) are:
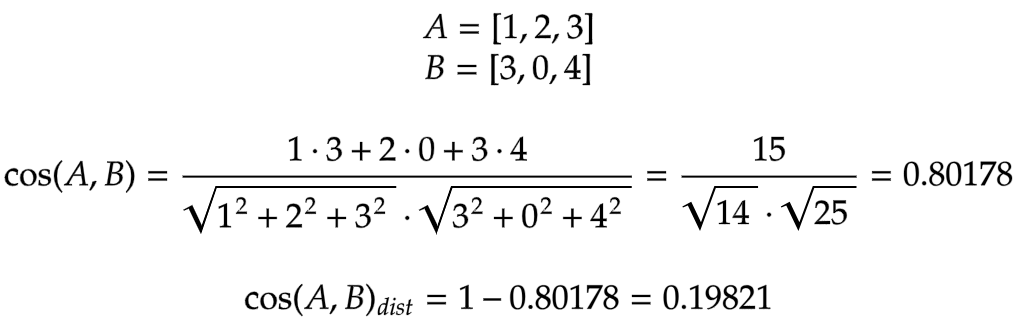
In PostgreSQL, the <=> operator computes the cosine distance.
select *, embedding <=> '[1,2,3]' as cosine_distance
from document
order by cosine_distance;+--+--------+------------------------------+---------+-------------------+
|id|name |content |embedding|cosine_distance |
+--+--------+------------------------------+---------+-------------------+
|1 |Raccoons|Raccoons are silly and funny. |[3,0,4] |0.19821627426272692|
|3 |Cats |Cats are funny and foxy. |[4,0,3] |0.30512077102769664|
|2 |Dogs |Dogs are friendly and helpful.|[5,0,2] |0.45407916631598844|
+--+--------+------------------------------+---------+-------------------+As cosine distance and cosine similarity are opposite, when working with cosine similarity, the results need to be ordered descending if the aim is to find more similar results.
select *, 1 - (embedding <=> '[1,2,3]') as cosine_similarity
from document
order by cosine_similarity desc;+--+--------+------------------------------+---------+------------------+
|id|name |content |embedding|cosine_similarity |
+--+--------+------------------------------+---------+------------------+
|1 |Raccoons|Raccoons are silly and funny. |[3,0,4] |0.8017837257372731|
|3 |Cats |Cats are funny and foxy. |[4,0,3] |0.6948792289723034|
|2 |Dogs |Dogs are friendly and helpful.|[5,0,2] |0.5459208336840116|
+--+--------+------------------------------+---------+------------------+To conclude, the cosine similarity measures how similar two vectors are, while the cosine distance, how different they are.
Enhancing the Search Speed
In the previous section, the aim was to find the vector embeddings that are closer to the chosen query vector – [1,2,3] – by using a specified distance metric. In order for such queries to be usable, they need to be fast. According to the documentation [Resource 1], pgVector uses by default the exact nearest neighbor search (kNN algorithms), which retrieves the nearest k vectors after comparing the queried one with each embedding in the database.
The complexity of kNN algorithms is O(n), thus scanning vectors with 200-300 dimensions against a large number of embeddings is computationally very expensive and not scalable.
The alternative is the Approximate Nearest Neighbor (ANN) approach which trades accuracy for a great deal of improvement in speed. pgVector supports two implementations:
Hierarchical Navigable Small World (HNSW)– creates an index based on a proximity graph (related vectors are stored next to one another)IVVFFlat– divides the vectors into lists and searches subsets of these that are closest to the queried one
There are plenty of details in the documentation [Resource 1] on how to parameterize, adjust, and monitor “the progress” of the execution when creating and using indexes that work based on these algorithms.
In the case of this analysis, HNSW indexes were created, one for each of the distance metrics used.
create index if not exists idx_l2_document_embedding on document
using hnsw (embedding vector_l2_ops)
with (m = 16, ef_construction = 64);
create index if not exists idx_ip_document_embedding on document
using hnsw (embedding vector_ip_ops);
create index if not exists idx_cosine_document_embedding on document
using hnsw (embedding vector_cosine_ops);Each of them may be parameterized with the maximum number of connections per layer and the size of the dynamic list of candidates when constructing the graph, respectively.
Takeaways
Vector databases play an important role in the AI context, as they are used to integrate self-data with the actual AI model and consequently transform it into a less stateless one.
For thorough and reliable results, there are a few important factors to take into account when choosing a metric. The actual data, the model used and the application type should be primarily taken into account. Then, the meaning of the metric is important in the concrete context.
Concerning the metrics analyzed in this article, from a cosine similarity point of view, two vectors are considered related if the angle between them is small, irrespective of their magnitude. On the other hand, the L2 distance between them might be substantial and discussions around the normalization of the data, loss functions, and fine-tuning might arise additionally in this case.
All in all, it is advisable to use the same (distance) metric as the one the ML model (the vectorizer, the entity that produces the embeddings) uses.
Resources
Published at DZone with permission of Horatiu Dan. See the original article here.
Opinions expressed by DZone contributors are their own.

Comments