Working With Irregular Time Series

One of the benefits of InfluxDB is the ability to store raw events, which might come in at varying intervals, as an irregular time series. However, irregular time series present some unique challenges, and in some cases, common operations on the data simply will not work. Fortunately, InfluxDB allows you to convert an irregular time series to a regular one on the fly by calculating an aggregate of individual values for arbitrary windows of time. This gives you the best of both worlds when capturing events from your systems and working with that data.

We can take a look at a few actual data points in order to get a better understanding of what considerations need to be made when working with irregular time series. For the sake of example, we'll use five data points, and give them values of 10, 20, 30, 40, and 50.

If this data if collected at regular intervals, then calculating the mean of the values will also give you the average power usage over time.

If your data is collected at irregular intervals, however, then calculating the mean of the values will not give you the expected results.

Adding those data points to InfluxDB and playing around with them will give us a better feel for what is going on. Using the Influx CLI, I inserted those five values into a measurement called m1:

> select * from m1 where time > '2018-08-14T17:22:14Z' and time < '2018-08-14T17:23:20Z'
name: m1
time                         value
----                         -----
2018-08-14T17:22:14.159637Z  10
2018-08-14T17:22:16.3561521Z 20
2018-08-14T17:22:18.2251241Z 30
2018-08-14T17:22:20.18086Z   40
2018-08-14T17:23:19.8976057Z 50

Since I inserted the data manually, the timestamps for the values are not evenly spaced, which is just what we want for this example. The first four occur during the same minute, while the fifth occurs nearly a minute later. We can calculate the mean of these five values:

> select mean(*) From m1
name: m1
time                 mean_value
----                 ----------
1970-01-01T00:00:00Z 30

and we get a result of 30, with the timestamp value in the result being the beginning of the time window for which we're calculating the mean.

If this were a regular time series, then an average value of 30 would make sense, intuitively. Because our example is an irregular time series, though, the amount of time between measurements matters when calculating the final result. This becomes more clear when visualizing the values; here is what those points look like on a graph:

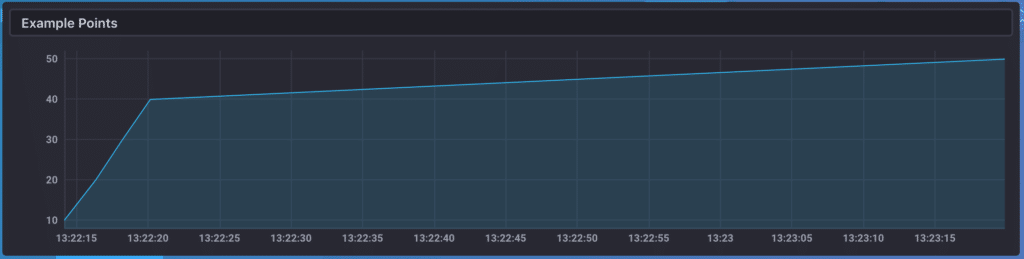
We can see that the majority of the time is spent between the value of 40 and the value of 50 (we're doing a linear interpolation between those points to draw a graph). We can make a reasonable guess, then, that the mean over time is probably closer to 40 than it is to 30.

Clearly, calculating the mean of all the values in an irregular series directly isn't going to work, since that operation ignores the values' distribution in time. We need to impose some kind of regularity on our data.

To do this, we can break up the time range for our data into discreet units using InfluxQL's GROUP BY clause, and then aggregate the values of the data within those windows. Not every interval will have a value, and those that do might have more than one value. We'll need to make a decision, as users and operators of our systems, about how we want to handle those cases. As is often the case when working with data, human judgement and interpretation play a significant role.

If we take small enough windows, and use the mean() function to calculate aggregates, we should get a fairly accurate representation of our time series. This is what our data looks like after we've grouped the points into ten-second intervals and calculated the mean for each group:

> select mean(*) from m1 where time > '2018-08-14T17:22:14Z' and time < '2018-08-14T17:23:20Z' group by time(10s)
name: m1
time                 mean_value
----                 ----------
2018-08-14T17:22:10Z 20
2018-08-14T17:22:20Z 40
2018-08-14T17:22:30Z 
2018-08-14T17:22:40Z 
2018-08-14T17:22:50Z 
2018-08-14T17:23:00Z 
2018-08-14T17:23:10Z 50

For the 10-second period beginning 2018-08-14T17:22:10Z, we have three values, 10, 20, and 30, and the mean of those is 20. For the next window, we have a single value, and then we have a number of windows with no value before we see the final value of 50. As before, we'll have to make a judgement call as to how we want to handle these empty windows.

The fill() option of GROUP BY will allow us to fill in data for any of those empty windows. fill() can take the options null, previous, number, none, or linear. In our case, linear is the right choice, since we graphed the values using linear interpolation, but if this were real data some of the other options might be more appropriate.

This is what our data looks like using fill(linear):

> select mean(*) from m1 where time > '2018-08-14T17:22:14Z' and time < '2018-08-14T17:23:20Z' group by time(10s) fill(linear)
name: m1
time                 mean_value
----                 ----------
2018-08-14T17:22:10Z 20
2018-08-14T17:22:20Z 40
2018-08-14T17:22:30Z 42
2018-08-14T17:22:40Z 44
2018-08-14T17:22:50Z 46
2018-08-14T17:23:00Z 48
2018-08-14T17:23:10Z 50

We can then calculate the mean of our new, regular time series, using subqueries:

> select mean(*) from (select mean(*) from m1 where time > '2018-08-14T17:22:14Z' and time < '2018-08-14T17:23:20Z' group by time(10s) fill(linear))
name: m1
time                 mean_mean_value
----                 ---------------
1970-01-01T00:00:00Z 41.42857142857143

There's another caveat, though: the window that we choose will have an impact on our final results. What if we use a 1s window instead of a 10s one?

> select mean(*) from (select mean(*) from m1 where time > '2018-08-14T17:22:14Z' and time < '2018-08-14T17:23:20Z' group by time(1s) fill(linear))
name: m1
time                 mean_mean_value
----                 ---------------
1970-01-01T00:00:00Z 42.95454545454546

We get a slightly different result! Working with irregular time series isn't exact, and your approach will vary depending on the data in question. Different methods of aggregation, interval size, and interpolation method will be more appropriate than others.

If the data in our examples above was some kind of environmental data, perhaps ambient temperature, and the irregularity of our series was due to unreliable data collection, then the approach we used might be appropriate.

If the data was instead collected whenever there was a state change, perhaps we have a number of LEDs and we're switching them on in blocks of ten, then the linear fill that we performed in the query no longer makes sense; instead, using fill(previous) would be more appropriate based on the behavior of the system that our data intends to model.

Ultimately, this is the biggest challenge in working with irregular time series: you need to understand your data well enough that you can make educated decisions about how to work with that data.