Human Introspection With Machine Intelligence

Computational logic manifests in various forms, much like other types of logic. In this paper, my focus will be on the abductive logic programming (ALP) approach within computational logic. I will argue that the ALP agent framework, which integrates ALP into an agent’s operational cycle, represents a compelling model for both explanatory and prescriptive reasoning. 

As an explanatory model, it encompasses production systems as a specific example; as a prescriptive model, it not only includes classical logic but also aligns with traditional decision theory. The ALP agent framework’s dual nature, encompassing both intuitive and deliberative reasoning, categorizes it as a dual-process theory. Dual-process theories, similar to other theoretical constructs, come in various versions. One such version, as Kahneman and Frederick [2002] describe, is where intuitive thinking “swiftly generates instinctive solutions to judgment issues,” while deliberative thinking “assesses these solutions, deciding whether to endorse, adjust, or reject them.” 

This paper will focus primarily on the prescriptive elements of the ALP agent framework, exploring how it can be utilized to enhance our cognitive processes and behaviors. Specifically, I will examine its potential to improve our communication skills and decision-making capabilities in everyday situations. I will assert that the ALP agent framework offers a solid theoretical basis for guidelines on effective writing in English, as outlined in [Williams, 1990, 1995], and for insights into better decision-making, as discussed in [Hammond et al., 1999]. The foundation for this paper lies in [Amin, 2018], which provides a detailed exploration of the technical aspects of the ALP agent framework, along with references to related scholarly work.

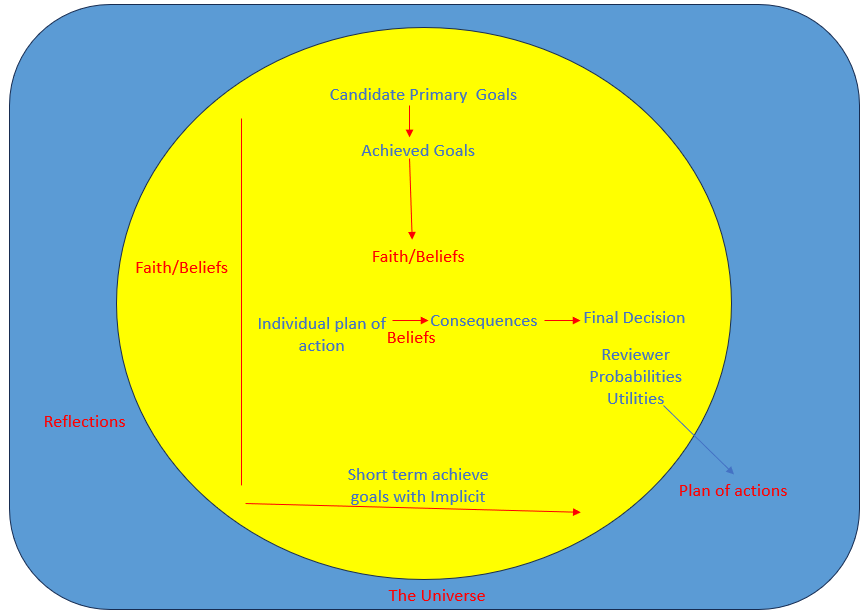
Streamlined Abductive Reasoning and Agent Loop

A Fundamental Overview of ALP Agents

The ALP agent framework can be considered a variation of the BDI (Belief-Desire-Intention) model, where agents leverage their knowledge to achieve their goals by forming intentions, which are essentially action plans. In ALP agents, both knowledge (beliefs) and objectives (goals) are represented as conditional statements in a logical form. Beliefs are expressed as logic programming rules, whereas goals are described using more flexible clauses, capable of capturing the full scope of first-order logic (FOL).

For example, the following statements illustrate this: The first one expresses a goal, and the subsequent four represent beliefs:

• If a crisis occurs, then I will either handle it myself, seek assistance, or escape the situation.
• A crisis arises if there is a breach in the ship.
• I seek assistance if I am on a ship and notify the captain.
• I notify the captain if I am on a ship and press the alarm button.
• I am on a ship.

In this discussion, goals are typically structured with conditions at the start, as they are primarily used for forward reasoning, similar to production rules. Beliefs, on the other hand, are generally structured with conclusions first, as they are often used for backward reasoning, akin to logic programming. However, in ALP, beliefs can also be written with conditions first, as they can be applied in both forward and backward reasoning. The specific order — whether forward or backward — does not affect the underlying logic.

Model Assumptions and Practical Language

In simpler terms, within the ALP agent framework, beliefs represent the agent’s view of the world, while goals depict the desired state of the world according to the agent. In a deductive database context, beliefs correspond to the stored data, and goals relate to queries or integrity rules.

Formally, in the model-theoretic interpretation of the ALP agent framework, an agent with beliefs BBB, goals GGG, and observations OOO must determine actions and assumptions such that G∪OG \cup OG∪O holds true within the minimal model defined by BBB. In the basic scenario where BBB consists of Horn clauses, BBB possesses a unique minimal model. Other, more complex scenarios can be simplified to this Horn clause case, though these technical aspects are beyond the primary focus here.

In the practical interpretation, ALP agents primarily reason forward based on their observations and Agents reason both forwards and backward from their beliefs to assess whether the conditions of a goal are satisfied and to determine the corresponding result as a target to achieve. Forward reasoning, similar to forward chaining in rule-based systems, involves making the conclusion of a goal true by ensuring its conditions are met. Goals that are interpreted this way are often referred to as maintenance goals. On the other hand, achievement goals are tackled by backward reasoning, which involves finding a sequence of actions that, when executed, will fulfill the goal. Backward reasoning operates as a process of goal decomposition, where actionable steps are treated as specific cases of atomic sub-goals.

For example, if I observe a fire, I can use the previously stated goals and beliefs to conclude through forward reasoning that an emergency exists, leading to the achievement goal of either handling the situation myself, seeking help, or escaping. These options form the initial set of possibilities. To achieve the goal, I can reason backward, breaking down the goal of seeking help into sub-goals like notifying the train driver and pressing the alarm button. If pressing the alarm button is an atomic action, it can be performed directly. If this action is successful, it fulfills the achievement goal and also satisfies the corresponding maintenance goal.

In model-theoretic terms, the agent must not only generate actions but also make assumptions about the world. This is where the concept of abduction comes into play in ALP. Abduction involves forming assumptions to explain observations. For instance, if I observe smoke instead of fire and have the belief that smoke implies fire, then backward reasoning from the observation will lead to the assumption that there is a fire. Forward and backward reasoning would then proceed as usual.

In both the model-theoretic and operational semantics, observations and goals are treated in a similar way. By reasoning both forward and backward, the agent generates actions and additional assumptions to make the goals and observations true within the minimal model of the world defined by its beliefs. In the earlier example, if the observation is that there is smoke, then the belief that there is fire and the action of pressing the alarm button, combined with the agent's beliefs, make both the goal and the observation true. The operational semantics align with the model-theoretic semantics, provided certain assumptions are met.

Selecting the Optimal Solution

There may be multiple solutions that, in conjunction with the set of beliefs BBB, make both goals GGG and observations OOO valid. These solutions may have varying outcomes, and the challenge for an intelligent agent is to identify the most effective one within the constraints of available resources. In classical decision theory, the worth of an action is determined by the expected benefit of its results. Similarly, in the philosophy of science, the value of an explanation is assessed based on its likelihood and its ability to account for observations (the more observations it can explain, the better).

In ALP agents, these same criteria can be applied to evaluate potential actions and explanations. For both, candidate assumptions are assessed by projecting their outcomes. In ALP agents, the process of finding the optimal solution is integrated into a backward reasoning strategy, utilizing methods like best-first search algorithms (e.g., A* or branch-and-bound). This approach is akin to the simpler task of conflict resolution in rule-based systems. Traditional rule-based systems simplify decision-making and abductive reasoning by converting high-level goals, beliefs, and decisions into lower-level heuristics and stimulus-response patterns. For instance:

• If there is a hole and I am on a ship, then I press the alarm button.

In ALP agents, lower-level rules can be combined with higher-level cognitive processes, akin to dual-process theories, to leverage the advantages of both approaches. Unlike most BDI agents, which focus on one plan at a time, ALP agents handle individual actions and can pursue multiple plans simultaneously to enhance the likelihood of success. For example, during an emergency, an agent might both activate the alarm and attempt to escape concurrently. The choice between focusing on a single plan or multiple plans at once depends on the chosen search strategy. While depth-first search focuses on one plan at a time, other strategies may offer greater benefits.

The ALP agent model can be utilized to create artificial agents, but it also serves as a useful framework for understanding human decision-making. In the following sections, I will argue that this model not only improves upon traditional logic and decision theory but also provides a normative (or prescriptive) approach. The case for adopting the ALP agent model as a foundation for advanced decision theory rests on the argument that clausal logic offers a viable representation of the language of thought (LOT). I will further explore this argument by comparing clausal logic with natural language and demonstrating how this model can aid individuals in clearer and more effective communication. I will revisit the application of the ALP agent model for enhancing decision-making in the final section.

Clausal Logic as an Agent's Cognitive Framework

In the study of language and thought, there are three primary theories about how language relates to cognition:

• Cognitive framework theory: Thought is represented by a private, language-like system that operates independently of external, spoken languages.
• Language influence theory: Thought is shaped by public languages, and the language we use influences our cognitive processes.
• Non-linguistic thought theory: Human thought does not follow a language-like structure.

The ALP agent model aligns with the first theory, disagrees with the second, and is compatible with the third. It diverges from the second theory because the ALP's logical framework does not depend on the existence of spoken languages, and, according to AI standards, natural languages are often too ambiguous to model human thought effectively. However, it supports the third theory due to its connectionist implementation, which masks its linguistic nature.

In AI, the idea that some form of logic represents an agent's cognitive framework is closely tied to traditional AI approaches (often referred to as GOFAI or "good old-fashioned AI"), which have been somewhat overshadowed by newer connectionist and Bayesian methods. I will argue that the ALP model offers a potential reconciliation between these different approaches. The clausal logic of ALP is simpler than standard first-order logic (FOL), incorporates connectionist principles, and accommodates Bayesian probability. It bears a relationship to standard FOL similar to how a cognitive framework relates to natural language.

The argument begins with relevance theory [Sperber and Wilson, 1986], which suggests that people understand language by extracting the most information with the least cognitive effort. According to this theory, the more a communication aligns with its intended meaning, the easier it is for the audience to grasp it. One way to investigate the nature of a cognitive framework is to examine scenarios where accurate and efficient understanding is crucial. For example, emergency notices on the London Underground are designed to be easily comprehensible because they are structured as logical conditionals, either explicitly or implicitly.

Actions To Take During an Emergency

To address a crisis, activate the alarm signal button to notify the driver. If any section of the train is at a station, the driver will stop. If not, the train will proceed to the next station where assistance can be more readily provided. Note that improper use of the alarm incurs a £50 penalty.

The first directive represents a procedural goal, with its logic encoded as a programming clause: activating the alarm will alert the captain. The second directive, while expressed in a logic programming form, is somewhat ambiguous and lacks a complete condition. It is likely intended to mean that the captain will halt the engine in a bay if alerted and if any part of the ship is present in the bay.

The third directive involves two conditions: the captain will stop the ship at the next dock if alerted and if no part of the ship is in a bay. The statement about providing assistance more easily if the ship is near the shore is an additional conclusion rather than a condition. If it were a condition, it would imply that the train stops only at stations where assistance is readily available.

The fourth directive is conditional in disguise: improper use of the alarm signal button may result in a £50 fine.

The clarity of the Emergency Notice is attributed to its alignment with its intended meaning in the cognitive framework. The notice is coherent, as each sentence logically connects with the previous ones and aligns with the reader’s likely understanding of emergency procedures.

The omission of conditions and specifics sometimes enhances coherence. According to Williams [1990, 1995], coherence can also be achieved by structuring sentences so that familiar ideas appear at the beginning and new ideas at the end. This method allows new information to seamlessly transition into subsequent sentences. The first three sentences of the Emergency Notice exemplify this approach.

Here is another illustration, reflecting the type of reasoning addressed by the ALP agent model:

• It is raining.
• If it is raining and you go out without an umbrella, you will get wet.
• If you get wet, you might catch a cold.
• If you catch a cold, you will regret it.
• You don’t want to regret it.
• Therefore, you should not go out without an umbrella.

In the next section, I will argue that the coherence demonstrated in these examples can be understood through the logical relationships between the conditions and conclusions within sentences.

Natural Language and Cognitive Representation

Understanding everyday natural language communications presents a more complex challenge compared to interpreting messages crafted for clarity and coherence. This complexity involves two main aspects. First, it requires deciphering the intended meaning of the communication. For instance, to grasp the ambiguous sentence "he gave her the book," one must determine the identities of "he" and "her," such as John and Mary.

The second challenge is to encode the intended meaning in a standardized format, ensuring that equivalent messages are represented consistently. For example, the following English sentences convey the same meaning:

• Alia gave a book to Arjun.
• Alia gave the book to Arjun.
• Arjun received the book from Alia.
• The book was given to Arjun by Alia.

Representing this common meaning in a canonical form simplifies subsequent reasoning. The shared meaning could be captured in a logical expression like give(Alia, Arjun, book), or more precisely as:

event(e1000).

act(e1000, giving).

agent(e1000, Alia).

recipient(e1000, Arjun).

object(e1000, book21).

Isa(book21, book).

The precise format helps distinguish between similar events and objects more effectively.

According to relevance theory, to enhance comprehension, communications should align closely with their mental representations. They should be expressed clearly and simply, mirroring the canonical form of the representation.

For example, instead of saying, "Every fish which belongs to class aquatic craniate has gills," one could say:

• "Every fish has gills."
• "Every fish belongs to the class aquatic craniate."
• "A fish has gills if it belongs to the class aquatic craniate."

In written English, clarity is often achieved through punctuation, such as commas around relative clauses. In clausal logic, this distinction is reflected in the differences between conclusions and conditions.

These examples suggest that the distinction and relationship between conditions and conclusions are fundamental aspects of cognitive frameworks, supporting the notion that clausal logic, with its conditional forms, is a credible model for understanding mental representations.

Comparing Standard FOL and Clausal Logic

In the realm of knowledge representation for artificial intelligence, various logical systems have been explored, with clausal logic often positioned as an alternative to traditional First-Order Logic (FOL). Despite its simplicity, clausal logic proves to be a robust candidate for modeling cognitive processes.

Clausal logic distinguishes itself from standard FOL through its straightforward conditional format while maintaining comparable power. Unlike FOL, which relies on explicit existential quantifiers, clausal logic employs Skolemization to assign identifiers to assumed entities, such as e1000 and book21, thereby preserving its expressive capabilities. Additionally, clausal logic surpasses FOL in certain respects, particularly when combined with minimal model semantics.

Reasoning within clausal logic is notably simpler than in standard FOL, predominantly involving forward and backward reasoning processes. This simplicity extends to default reasoning, including handling negation by failure, within the framework of minimal model semantics.

The relationship between standard FOL and clausal logic mirrors the relationship between natural language and a hypothetical Language of Thought (LOT). Both systems involve two stages of inference: the first stage transforms statements into a standardized format, while the second stage utilizes this format for reasoning.

In FOL, initial inference rules such as Skolemization and logical transformations (e.g., converting ¬(A ∨ B) to ¬A ∧ ¬B) serve to convert sentences into clausal form. Subsequent inferences, such as deriving P(t) from ∀X(XP(X)), involve reasoning with this clausal form, a process integral to both forward and backward reasoning.

Much like natural language offers multiple ways to convey the same information, FOL provides numerous complex representations of equivalent statements. For instance, the assertion that "all fish have gills" can be represented in various ways in FOL, but clausal logic simplifies this to a canonical form, exemplified by the clauses: gills(X) ← fish(X) and fish(Alia).

Thus, clausal logic relates to FOL in a manner akin to how the LOT relates to natural language. Just as the LOT serves as a streamlined and unambiguous version of natural language expressions, clausal logic offers a simplified, canonical version of FOL. This comparison underscores the viability of clausal logic as a foundational model for cognitive representation.

In AI, clausal logic has proven to be an effective knowledge representation framework, independent of the communication languages used by agents. For human communication, clausal logic offers a means to express ideas more clearly and coherently by aligning with the LOT. By integrating new information with existing knowledge, clausal logic facilitates better coherence and understanding, leveraging its compatibility with connectionist representations where information is organized in a network of goals and beliefs [Aditya Amin, 2018].

A Connectionist Interpretation of Clausal Logic

Just as clausal logic reformulates First-Order Logic (FOL) into a canonical form, the connection graph proof procedure adapts clausal logic through a connectionist framework. This approach involves precomputing and establishing connections between conditions and conclusions, while also tagging these connections with their respective unifying substitutions. These pre-computed connections can then be activated as needed, either forward or backward. Frequently activated connections can be streamlined into shortcuts, akin to heuristic rules and stimulus-response patterns.

Although clausal logic is fundamentally a symbolic representation, once the connections and their unifying substitutions are established, the specific names of the predicate symbols become irrelevant. Subsequent reasoning primarily involves the activation of these connections and the generation of new clauses. The new clauses inherit their connections from their predecessors, and in many cases, outdated or redundant parent clauses can be discarded or overwritten once their connections are fully utilized.

Connections can be activated at any point, but typically, it is more efficient to activate them when new clauses are introduced into the graph as a result of fresh observations or communications. Activation can be prioritized based on the relative significance (or utility) of observations and goals. Additionally, different connections can be weighted based on statistical data reflecting how often their activation has led to beneficial outcomes in the past.

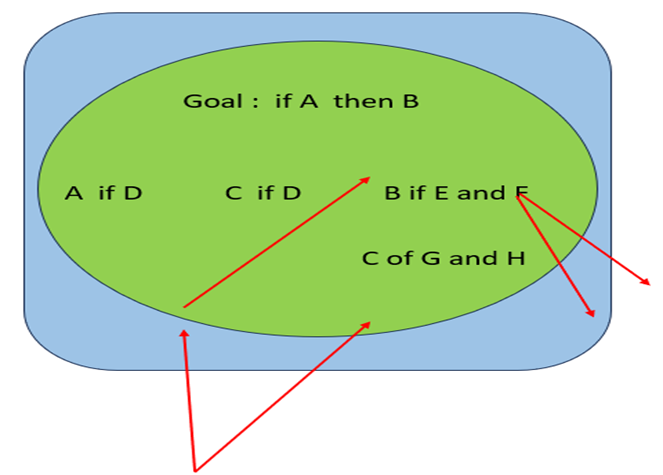
Figure 2: A simplified connection graph illustrating the relationships between goals and beliefs.

Notice that only D, F, and H are directly linked to real-world elements. B, C, and A are cognitive constructs used by the agent to structure its thoughts and manage its actions. The status of E and G remains undefined. Additionally, a more direct approach is achievable through the lower-level goal if D then ((E and F) or (G and H)).

Observation and goal strengths are distributed across the graph according to link weights. The proof procedure, which activates the most highly weighted links, resembles Maes’ activation networks and integrates ALP-style forward and backward reasoning with a best-first search approach.

Although the connection graph model might suggest that thinking lacks linguistic or logical attributes, the difference between connection graphs and clausal logic is akin to the distinction between an optimized, low-level implementation and a high-level problem representation.

This model supports the notion that thought operates within a LOT independent of natural language. While the LOT may aid in developing natural language, it is not contingent upon it.

Moreover, the connection graph model implies that expressing thoughts in natural language is comparable to translating low-level programs into higher-level specifications. Just as decompiling programs is complex, this might explain why articulating our thoughts can be challenging.

Quantifying Uncertainty

In assembly graphs, there are internal links that organize the agent’s cognitive processes and external links that connect these processes to the real world. External links are activated through observations and the agent’s actions and may also involve unobserved world properties. The agent can formulate hypotheses about these properties and assess their likelihood.

The probability of these hypotheses influences the expected outcomes of the agent’s actions. For instance:

• You might become wealthy if you purchase a raffle ticket and your number is selected.
• Rain might occur if you perform a rain dance and the deities are favorable.

While you can control certain actions, such as buying a ticket or performing a rain dance, you cannot always influence others' actions or global conditions, like whether your number is chosen or the gods are pleased. At best, you can estimate the probability of these conditions being met (e.g., one in a million). David Poole [1997] demonstrated that integrating probabilities with these assumptions equips ALP with capabilities similar to those of Bayesian networks.

Enhanced Decision-Making

Navigating uncertainty about the world presents a significant challenge in decision-making. Traditional decision theory often simplifies this complexity by making certain assumptions. One of the most limiting assumptions is that all possible choices are predefined. For instance, when seeking a new job, classical decision theory assumes that all potential job opportunities are known in advance and focuses solely on selecting the option likely to yield the best outcome.

Decision analysis offers informal strategies to improve decision-making by emphasizing the goals behind various options. The ALP agent model provides a structured approach to formalize these strategies, integrating them with a robust model of human cognition. Specifically, it demonstrates how expected utility —  a cornerstone of classical decision theory — can also guide the exploration of alternatives through best-first search techniques. Furthermore, it illustrates how heuristics and even stimulus-response patterns can complement logical reasoning and decision theory, reflecting the principles of dual process models.

Conclusions

This discussion highlights two key ways the ALP agent model, drawing from advancements in Artificial Intelligence, can enhance human intellect. It aids individuals in articulating their thoughts more clearly and coherently while also improving decision-making capabilities. I believe that applying these methods represents a promising research avenue, fostering collaboration between AI experts and scholars in humanistic fields.

References

[1] [Carlson et al., 2008] Kurt A. Carlson, Chris Janiszewski, Ralph L. Keeney, David H. Krantz, Howard C. Kunreuther, Mary Frances Luce, J. Edward Russo, Stijn M. J. van Osselaer and Detlof von Winterfeldt. A theoretical framework for goal-based choice and for prescriptive analysis. Marketing Letters, 19(3-4):241- 254.

 [2] [Hammond et al., 1999] John Hammond, Ralph Keeney, and Howard Raiffa. Smart Choices - A practical guide to making better decisions. Harvard Business School Press.

[3] [Kahneman, and Frederick, 2002] Daniel Kahneman and Shane Frederick. Representativeness revisited: attribute substitution in intuitive judgment. In Heuristics and Biases – The Psychology of Intuitive Judgement. Cambridge University Press.

[4] [Keeney, 1992] Ralph Keeney. Value-focused thinking: a path to creative decision-making. Harvard University Press.

[5] [Maes, 1990] Pattie Maes. Situated agents can have goals. Robot. Autonomous Syst. 6(1-2):49-70.

[6] [Poole, 1997] David Poole. The independent choice logic for modeling multiple agents under uncertainty. Artificial Intelligence, 94:7-56.