Feature Hashing for Scalable Machine Learning

Feature hashing is a powerful technique for handling sparse, high-dimensional features in machine learning. It is fast, simple, memory-efficient, and well-suited to online learning scenarios. While an approximation, it has surprisingly low accuracy tradeoffs in many machine learning problems.

In this post, I will cover the basics of feature hashing and how to use it for flexible, scalable feature encoding and engineering. I'll also mention feature hashing in the context of Apache Spark's MLlib machine learning library. Finally, I will explore the performance and scalability characteristics of feature hashing on some real datasets.

Introduction to Feature Hashing

Almost all machine learning algorithms are trained using data in the form of numerical vectors called feature vectors. However, a large proportion of useful training data does not come neatly packaged in vector form. Instead, our data may contain categorical features, raw text, images, etc.

Before it can be used for training a machine learning algorithm, this raw data must be transformed into feature vectors through the process of feature extraction or encoding.

For example, the one-hot encoding scheme is popular for categorical features, while bag-of-words is a commonly used (and similar) approach for text.

Even raw numerical features are often more informative when transformed into categorical form. For example, think about bucketing age into ranges or time into periods of the day such as morning, afternoon, and evening, or raw geo-location into country, region, and city. Bucketing or binning numerical variables in this way is a common feature extraction technique and once the features are in this form, we can simply apply the standard categorical one-hot encoding.

Dealing With Sparse, High-Dimensional Features

Many domains have very high feature dimension (the number of features or variables in the dataset), while some feature domains are naturally dense (for example, images and video). Here, we're concerned with sparse, high-cardinality feature domains such as those found in online advertising, e-commerce, social networks, text, and natural language processing.

By high-cardinality features, we mean that there are many unique values that the feature can take on. Feature cardinality in these domains can be of the order of millions or hundreds of millions (for example, the unique user IDs, product IDs, and search keywords in online advertising). Feature sparsity means that for anyone training example the number of active features is extremely low relative to the feature dimension — this ratio is often less than 1%.

This creates a challenge at scale because even simple models can become very large, making them consume more memory and resources during training and when making predictions in production systems. It's natural to think about applying some form of dimensionality reduction in this scenario — and this is where feature hashing comes in.

The "Hashing Trick"

The core idea behind feature hashing is relatively simple: Instead of maintaining a one-to-one mapping of categorical feature values to locations in the feature vector, we use a hash function to determine the feature's location in a vector oflower dimension.

For example, one-hot encoding would assign a unique index in the feature vector to each possible feature value, so a feature with one million possible values would equate to a vector size of one million (that is, one index into the vector for each feature value). By contrast, if we use feature hashing, that same feature with one million possible values could be hashed into a vector with dramatically smaller size — say, 100,000, or even 10,000.

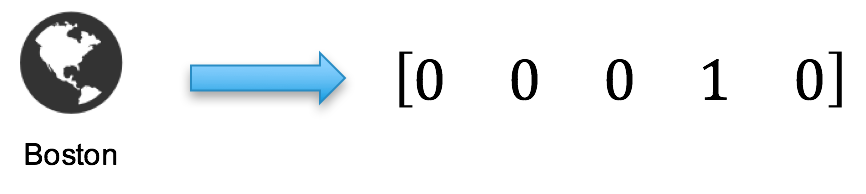
To determine the vector index for a given feature value, we apply a hash function to that feature value (say, city=Boston) to generate a hash value. We then effectively project that hash value into the lower size of our new feature vector to generate the vector index for that feature value (using a modulo operation).

The same idea applies to dealing with text — the feature indices are computed by hashing each word in the text, while the only difference is that the feature values represent counts of the occurrence of each word (as in the bag-of-words encoding) instead of binary indicators (as in the one-hot encoding). In order to ensure the hashed feature indices are evenly spread throughout the vector, the hashed dimension is typically chosen to be a power of 2 (where the power is referred to as the number of hash bits).

When using hashing combined with the modulo operation, we may encounter hash collisions — this occurs when two feature values end up being hashed to the same index in the vector. It turns out that in practice for sparse feature domains, this has very little impact on the performance characteristics of our machine learning algorithm. The reasoning behind this is that for very sparse features, relatively few tend to be informative, and in aggregate we hope that any hash collisions will impact less informative features. In a sense, hash collisions add a type of "noise" to our data — and our machine learning algorithms are designed to pick out the signal from the noise, so their predictive accuracy doesn't suffer too much.

Using feature hashing, we can gain significant advantages in memory usage since we can bound the size of our feature vectors and we don't need to store the exact one-to-one mapping of features to indices that are required with other encoding schemes. In addition, we can do this very fast, with little loss of accuracy, while preserving sparsity. Because of these properties, feature hashing is well-suited to online learning scenarios, systems with limited resources, or when speed and simplicity are important.

Of course, these benefits come at a cost. In addition to the potential for hash collisions mentioned above, we lose the ability to perform the inverse mapping from feature indices back to feature values, precisely because we don't generate or store the explicit feature mapping during feature extraction. This can be problematic for inspecting features (for example, we can compute which features are most informative for our model, but we are unable to map those back to the raw feature values in our data for interpretation).

Feature Hashing in Spark

Feature hashing has been made somewhat popular by open-source machine learning toolkits including Vowpal Wabbit and scikit-learn. Apache Spark's MLlib machine learning library currently supports feature hashing for text data using the HashingTF feature transformer. However, it's not possible to use this functionality directly for categorical features, forcing us to use workarounds that don't fit neatly into MLlib's pipelines. I go into some detail on this, as well as the proposed FeatureHasher for Spark, in my Spark Summit East 2017 talk.

Experimental Results

Above I claimed that feature hashing doesn't cost much in terms of model performance. Does this hold up to some real data? To answer this, I evaluated the impact of using feature hashing for text and high-cardinality categorical features. The datasets used are for binary classification, using AUC (area under the ROC curve) as the evaluation metric.

The first dataset is from a Kaggle Email Spam Classification competition. It contains the email text content for around 2500 spam and non-spam emails. The data size is not large but just serves to illustrate the impact of feature hashing for encoding text features. The baseline, in this case, is the "full" bag-of-words encoding (the vocabulary size after basic tokenization is around 50,000). We compare feature hashing, varying the number of hash bits, with the baseline, using a simple logistic regression model (in this case, MLlib's LogisticRegression with default settings except for adding a little regularization).

We can see in the chart that the AUC for feature hashing is very slightly less than for the baseline, but the difference is marginal.

The next two datasets are taken from ad click competitions from Criteo and Outbrain. These contain a relatively small number of features, but these features have extremely high cardinality — the total feature dimensions are around 34 million and 15 million, respectively. The data is also extremely sparse (of the order of 0.00001% sparsity).

Again, we vary the number of hash bits and evaluate the impact on performance. The results are a little noisy, but we can see that the impact on classification performance of using lower hash bits is negligible, especially relative to the speed and memory efficiency gains we get from the smaller vector size. For example, in the case of the Criteo data, we can effectively shrink our feature dimension from 34 million down to 262,144 (2¹⁸) — a significant reduction at a very little cost in terms of performance!

Conclusion

In this post, I introduced feature hashing as a fast, efficient, flexible technique for feature extraction that can scale to sparse, high-dimensional data without giving up much accuracy. Feature hashing is a valuable tool in the data scientist's arsenal, and I encourage you to try it out, and watch and comment on the relevant Spark JIRA to see it in Apache Spark soon!