Efficient Transformer Attention for GenAI

Generative AI (aka GenAI) is transforming the world with a plethora of applications including chatbots, code generation, and synthesis of images and videos. What started with ChatGPT soon led to many more products like Sora, Gemini, and Meta-AI. All these fabulous applications of GenAI are built using very large transformer-based models that are run on large GPU servers. But as the focus now shifts towards personalized privacy-focused Gen-AI (e.g., Apple Intelligence), researchers are trying to build more efficient transformers for mobile and edge deployment.

Transformer-based models have become state of the art in almost all applications of natural language processing (NLP), computer vision, audio processing, and speech synthesis. The key to the transformer's ability to learn long-range dependencies and develop a global understanding is the multi-head self-attention block. However, this block also turns out to be the most computationally expensive one, as it has quadratic complexity in both time and space. Thus, in order to build more efficient transformers, researchers are primarily focusing on:

• Creating linear complexity attention blocks using the kernel trick
• Reducing the number of tokens that take part in attention
• Designing alternate mechanisms for attention

In this article, we shall go through these approaches to provide an overview of the progress towards efficient transformer development.

Multi-Head Self Attention (MHSA)

In order to discuss efficient transformer design, we have to first understand the Multi-Head Self Attention (MHSA) block introduced by Vaswani et al. in their groundbreaking paper “Attention Is All You Need." In MHSA, there are several identical self-attention heads and their outputs are concatenated at the end. As illustrated in the figure below, each self-attention head projects the input x into three matrices — queries Q, keys K, and values V of sizes — N x d where N is the number of tokens and d denotes the model dimension. Then, the attention, A computes the similarity between queries and keys and uses that to weigh the value vectors. 

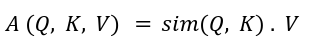
In MHSA, scaled-softmax is used as the similarity kernel:

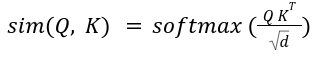
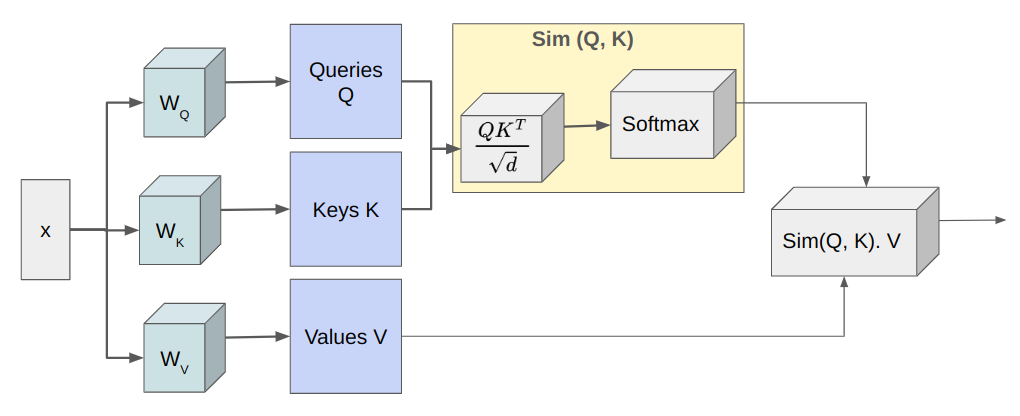
Computing the dot product of Q and K is of complexity O (N^2 d), so the latency of MHSA scales poorly with N. For images, N = HW where H and W are the height and width of the image. Thus, for higher-resolution images, latency increases significantly. This quadratic complexity is the biggest challenge in the deployment of these vanilla transformer models on edge devices. The next three sections elaborate on the techniques being developed to reduce the computational complexity of self-attention without sacrificing performance.

Linear Attention With Kernel Trick

Softmax attention is not suited for linearization. Hence, several papers have tried to find a suitable decomposable similarity kernel that can allow changing the order of matrix multiplication to reduce latency. Let's say, for some feature representation function F(x), such that:

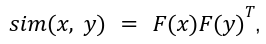
We can obtain similarity kernel as: 

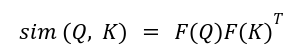
So that the attention can be written as:

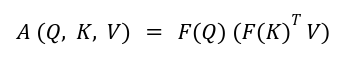
By first multiplying Key and Value matrices, we reduce the complexity to be O (N d^2), and if N << d, then the complexity of attention operation is reduced from quadratic to linear.

The following papers choose different feature representation functions F(x) to approximate the softmax attention and try to achieve similar or better performance than the vanilla transformer but for a fraction of time and memory costs.

1. Elu Attention

The "Transformers are RNNs" paper selected the following feature representation function to obtain a positive similarity matrix:

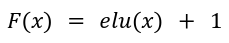
Where elu(x) is exponential linear unit with  a > 0 defined as:

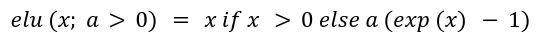
They chose elu(x) over ReLU(x) as they didn’t want the gradients to be zero when x < 0. 

2. Cosine Similarity Attention

The cosFormer paper recognized that softmax dot-product attention has the capacity to learn long-range dependencies. The authors attributed this capacity to two important properties of the attention matrix: first, the attention matrix is non-negative, and second, the attention matrix is concentrated by a non-linear re-weighting scheme. These properties formed the basis of their linear replacement for the softmax attention.

In order to maintain the non-negativity of the attention matrix, the authors used ReLU as a transformation function and applied it to both query Q and key K matrices. After that, cosine re-weighing was done as cos puts more weights on neighboring tokens and hence, enforces locality.

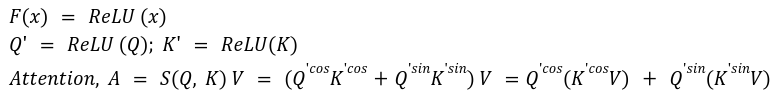
3. Hydra Attention

The Hydra Attention paper also used the kernel trick to first change the order of multiplication of matrices. The authors extended the multi-head concept to its extreme and created as many heads as the model dimension d. This allowed them to reduce the attention complexity to O (Nd). 

Hydra attention involves an element-wise product between Key and Value matrices and then sums up the product matrix to create a global feature vector. It then uses the Query matrix to extract the relevant information from the global feature vector for each token as shown below.

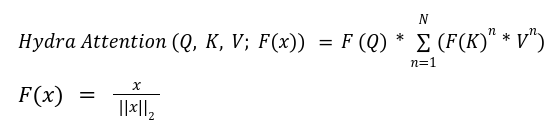
Where * represents the element-wise product and the function F(x) in Hydra attention is L2-Normalization so that the attention matrix is basically cosine similarity. The summation represents combining information from all heads.

4. SimA Attention

The SimA paper identified that in the regular attention block, if a channel in the Q or K matrix has large values, then that channel can dominate the dot product. This issue is somewhat mitigated by multi-head attention. In order to keep all channels comparable, the authors chose to normalize each channel of Q  and K by the L1-Normalization along the channel dimension. Thus, L1-Normalization is used as the feature representation function to replace the softmax function. 

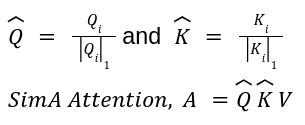
Where the order of multiplication depends on if N > d or N < d.

Further, unlike vanilla transformer architectures, the interactions between query and key are allowed to be negative. This signifies that one token can potentially negatively affect another token. 

Reducing the Number of Tokens

This class of papers focuses on reducing the number of tokens, N, that take part in the attention module. This helps to reduce the number of computations while still maintaining the same model performance. Since the computational complexity of multi-head self-attention is quadratic in N; hence, this approach is able to bring some efficiency into transformer models. 

1. Swin Transformer

Swin Transformer is a hierarchical transformer architecture that makes use of shifted-window attention. The hierarchical structure is similar to convolutional models and introduces multi-scale features into transformer models. The attention is computed in non-overlapping local windows which are partitions of an image. The number of image patches in a window partition is fixed, making the attention’s complexity linear with respect to the image size.  

The attention mechanism of the Swin Transformer is composed of Window-Multihead Self Attention (W-MSA) followed by Shifted Window-Multihead Self Attention module (SW-MSA). Each of these attention modules applies self-attention in a fixed window partition of size M x M which is independent of image resolution. Only in the case of SW-MSA, windows are shifted by M/2, which allows for cross-window connections and increases the modeling power. Since M is constant, the computational complexity becomes linear in the number of image patches (tokens). Thus, the Swin transformer builds a more efficient transformer by sacrificing global attention but it limits the model’s capacity to have a very long-range understanding. 

2. ToSA: Token Selective Attention

The ToSA paper introduced a new Token-Selector module that uses attention maps of the current layer to select “important” tokens that should participate in the attention of the next layer. The remaining tokens are allowed to bypass the next layer and are simply concatenated with the attended tokens to form the complete set of tokens. This Token-Selector can be introduced in alternate transformer layers and can help reduce the overall computations. However, this model’s training mechanism is quite convoluted involving multiple stages of training.

Alternate Attention Mechanisms

This class of papers attempts to replace the multi-head self-attention with more scalable and efficient attention mechanisms. They generally make use of convolutions and reordering of operations to reduce computational complexity. Some of these approaches are described below.

1. Multi-Scale Linear Attention

The EfficientViT paper also used the kernel trick to reduce the computational complexity of the transformer block to linear in the number of tokens. The authors selected ReLU as the feature transformer function F(x). However, they noticed that ReLU creates quite diffused attention maps compared to Softmax Scaled Dot-Product attention. Hence, they introduced small-kernel depth-wise convolutions applied individually to Query Q, Key K, and Value V matrices followed by ReLU Attention to better capture the local information. In total, this attention block involves three ReLU attentions one each on - Q, K, and V, 3x3 DepthWise-Conv of Q, K, V and 5x5 DepthWise-Conv of Q, K, V. Finally, the three outputs are concatenated.

2. Transposed Attention

The EdgeNeXt paper preserved the transformer's capacity to model global interactions by keeping the dot-product attention. However, the paper used a transposed version of attention, wherein the 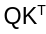 is replaced by: 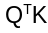This changes the dot-product computation from being applied across spatial dimensions to being applied across channel dimensions. This matrix is then multiplied with values V and then summed up. By transposing the dot product, the authors reduce the computation complexity to be linear in the number of tokens.

3. Convolutional Modulation

The Conv2Former paper simplified the attention mechanism by using a large kernel depth-wise convolution to generate the attention matrix. Then, element-wise multiplication is applied between the attention and value matrices. Since there is no dot product, computational complexity is reduced to linear. However, unlike MHSA, whose attention matrix can adapt to inputs, convolutional kernels are static and lack this ability.

4. Efficient Additive Attention

The SwiftFormer paper tried to create a computationally inexpensive attention matrix that can learn global interactions and correlations in an input sequence. This is achieved by first projecting the input matrix x into query Q and key K matrices. Then, a learnable parameter vector is used to learn the attention weights to produce a global attention query q. Finally, an element-wise product between q and K captures the global context. A linear transformation T is applied to the global context and added to the normalized query matrix to get the output of the attention operation. Again, as only element-wise operations are involved, the computational complexity of attention is linear.

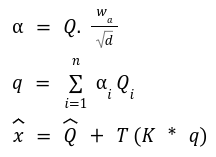
The Road Ahead

Developing efficient transformers is essential for getting the best performance on edge systems. As we move towards more personalized AI applications running on mobile devices, this is only going to gain more momentum. Although considerable research has been done, however, a universally applicable efficient transformer attention with similar or better performance than Multi-Head Self Attention is still an open challenge. However, for now, engineers can still benefit from deploying one or more of the approaches covered in this article to balance performance and efficiency for their AI applications.