Data Structures and Indexing for Operations on Deeply Nested Comments
In this post I demonstrate a schema, an entity, a DTO, and a continuous fraction index, for JPQL-only CRUD operations on deeply nested comments in relational databases.
Join the DZone community and get the full member experience.
Join For FreeYou may wonder if this problem is still relevant in 2020. The answer is: very much so! Despite the great success of Neo4j, a graph database, and other NoSQL databases, such databases are still rarely seen in non-startup Spring Boot projects. So, if you are a Java developer, who works on such a project, and are looking for a JPQL-only solution for this problem, the proposed approach may be helpful for you.
This post demonstrates the data structure and algorithms, analyzes their complexity, and reviews the literature. If you are looking for an actual Spring Initializr project. So, let us start.
The Requirements
We will build a CRM system for a mid-size online education center. The system is implemented with Spring Boot 2, H2 (development), and (for now) Ms-SQL(production) technology. Among many functionalities, the system must be able to create, read, update, and delete nested comments from/to a relational database. The functional requirements for the comment functionality are:
- The most common operations are to find all descendants of a particular comment and to find all root comments,
- All new and edited comments are moderated before being published and saved into the database,
- If a comment is deleted, all its child comments are deleted as well,
- The system should support full-text search over comments' content.
We assume the following about the comments:
- The comments are text strings no more than a certain length (no pictures or video fragments for now),
- Every comment has 0 or 1 parent,
- Most of the comments are questions/answers/hints on assignments and classes, so there going to be a lot more reads than writes,
- Ones saved, the comments are rarely updated and even more rarely, if ever, deleted,
- The older the comment gets, the lesser it is commented; the total number of child comments of a particular comment rarely exceeds a certain (large) number; the number depends on the depth of the comment.
- For every root comment, there are hundreds or more sub root comments. This can be achieved if only users of a certain role or reputation can create root comments.
- The majority of the comments are just few level deep. Much deeper comments are rare.
The following are the implementation details for the comment functionality:
- The functionalities need to be implemented with JPQL only and no native queries,
- There should be as few pessimistic locks as possible.
These requirements are not easy to satisfy simultaneously.
The Challenges
To implement these requirements, we face the following challenges:
- The data structures must be compatible with the relational database (rows and columns), yet implement a deeply nested tree.
- There should be efficient indexes to quickly find all children of a particular comment, yet no dialect-specific database features should be used.
- If all comments are stored in a single table, all root comments can not be found quickly without advanced dialect-specific database features. Yet, if all root comments are stored in a separate table, we have to use transactions. (this challenge is addressed in Part 2).
Let's start with the data structures. According to the book by Joe Celko, there are 3 major data structures for hierarchical data in relational databases:
- Adjacency list: each element has a reference to its immediate parent; root elements have a null parent. To find all descendants of a particular element, one needs to use "WITH RECURSION"-like clause. However, the clause is not supported in Spring Data JPQL. Other options, like
@OneToManyself-reference or@NamedEntityGraphsannotations, either make too many separate SELECT calls or don't work recursively (see this post of Juan Vimberg for details). So this approach alone is not enough for our requirements, but let's keep it in mind. - Enumerated path (AKA materialized path): every element keeps the information about all its ancestors. For example, if the node with id=n3 has its parent id=n2 and its grandparent id=n1, then n3 has a string "n1.n2.n3", where "." is a delimiter. To naively find all descendants of a node n3, for example, we need to do a SELECT call with LIKE "n1.n2.n3.%". This is an extremely costly operation because we need to scan the whole table of comments and it takes a long time to compare strings. This approach will do, but we need a faster index.
- Nested sets & nested intervals: every node has two numbers - left and right; the numbers make up an interval. All descendants of this node have their intervals within their ancestor's intervals. This data structure allows us to find all descendants very quickly, but makes inserts and deletes extremely slow (see this post for details and this post for benchmarks). So, this approach on its own is not enough for us either, but it gives a valuable clue on how to index our data.
Out of these 3 approaches, we will use the materialized path as the primary one and mix it with the other two. Let's see why it is not easy to index the materialized path.
At first glance, the alphabetical string index is ideal for the materialized path data structure. However, to our knowledge, such an index can't be made with JPQL only. Indeed, an alphabetically ordered tree can't be a B-tree, since the later is balanced and the former is not, so we can't use out of the box functionality to construct such an index. Worse still, it takes a much longer time to compare two strings then to compare two numbers.
A full-text index can be an option (see this post, where this approach is investigated), but there can be only 1 full-text index per table, so we need to keep it for full-text search over comments content. If we compose a full-text index out of the comment path and comment content columns, there going to be a lot of irrelevant string comparisons. So, let's see how to encode materialized path strings with numbers.
The Solution
Our solution consists of a schema, an ORM entity, a data transfer object, an algorithm to generate paths, an algorithm to compute indexes and index brackets, and an algorithm to resolve collisions.

The schema is shown in Fig 1(left). Obvious features, like NOT NULL for the PK, are omitted for brevity. Here, we use a single table for both comment content and comment hierarchy information to make searches and inserts quicker. Here we combine the materialized path and the adjacency list approaches: the row contains both its parent_id and the path to its ancestors. Also, every row contains its depth- the number of ancestors + 1; for the root comments depth=1.
Notice the index field of type DECIMAL(38,28). This means the float point number has 38 digits total and 28 digits for its fractional part. 38 is the max precision in Ms-SQL. Such numbers are well suited for an out of the box B-tree index in any relational database. The details of how to compute the index are discussed below. Finally, the id is AUTO_INCREMENTed.
The ORM entity is also shown in Fig 1(center). Obvious field-column mappings, no-arg, full arg constructors are omitted for brevity. DECIMAL index from the Comments table is mapped to the BigDecimal index field. Also, there is a constructor to build the Comment entities from the CommentDto.
Next, there are no self-referencing @OneToMany annotations. As was mentioned before, Spring Boot makes a lot of separate SELECT calls to the database to fulfill this annotation.
At last, CommenDto is shown in Fig 1(right). Immediate children of every node are referred to in the List<CommentDto> children field. Also, there is a constructor to build a CommentDto instance out of a Comment entity. So, how to generate a path and compute the index?
To generate the path of a comment, we use the following rules:
- For a root comment, the path is the auto-generated id of the element. For example, if
id=123456789, thenpath="123456789". - For a next to root comment (depth=2), we generate a random number X from 1 to M1 - a large enough number from the assumption 5. Then
path="Root_id.X", where Root_id is the id of the parent. Notice, that X has nothing to do with the sub-comment auto-generated id. - For deeper comments (depth>2), we again generate a random number X from 1 to Md - a large enough number from the assumption 5. Then
path="Parent_path.X", whereParent_pathis the comment's parent path. Again, X has nothing to do with the comment's auto-generated id.
Now comes the tricky part - how to compute the index and index brackets of a path string. For this, we need to recall continuous fractions (see this great paper of Vladimir Topashko for details). Every path string A corresponds to a semi-opened interval (Fig 2, A) [I(1,A),I(inf,A)[ ,or ]I(inf,A),I(1,A)] depending on which is smaller.

This property follows from the fact that the function I(x, A) gets its extrema at x=1 and x=inf. The main proposition of the paper is that every descendant interval is within its ancestor interval. Fig 2 (B) illustrates this proposition for the paths "3" and "3.X". The interval of "3" is ]3+r,4] where r->0. The child intervals of "3.X" are within their parent interval. Now, how can we assert that element B is a descendant of element A?
Element B is a descendant of element A if I(x, B) is within the interval of A for any x from 1 to inf. Theoretically, it doesn't matter which x to choose, since the interval of B is within the interval of A. However, to avoid ambiguity due to rounding errors, lets set x=2 and call I(2, A) the index of string A. In this case, the index is guaranteed to be strictly within the interval.
The price we pay is that ancestor indexes may be within their descendants' intervals and we need to filter the ancestors out from the descendants (see below). How to actually compute the index?
The index computation algorithm is as follows:
xxxxxxxxxx
public BigDecimal computeIndex(List<BigDecimal> longPath){
MathContext mc = new MathContext(128,RoundingMode.HALF_UP);
BigDecimal half = new BigDecimal("0.5");
half = half.setScale(128, RoundingMode.HALF_UP);
int pathLength = longPath.size();
if(pathLength==1){
return longPath.get(0).add(half,mc);
}
BigDecimal tempInd = longPath.get(pathLength-1).add(half,mc);
for(int i=pathLength-2;i>=0;i--){
tempInd = longPath.get(i).add(one.divide(tempInd, mc),mc);
}
return tempInd;
}
The input longPath is a path string, where all numbers are converted to BigDecimals. For example: "12345.678.90" is converted to [12345,678,90]. The algorithm computes the index according to the recurrent formula in Fig 2 (A) with x=2. Notice the MathContext object at line 2. It is important for this algorithm to carefully specify the precision and rounding mode.
Indeed, if we round float point numbers "half-up", the rounding error behaves like a Brownian particle. Its "displacement" is proportional to the square root of the number of operations. On the other hand, if we simply discard "less significant" digits, we introduce a systematic downward drift, like a gravity field; in this case, the "displacement" increases linearly with the number of operations.
Next, we need to compute the interval brackets. Let's call them "bra" and "ket". "Bra" is computed as follows:
xxxxxxxxxx
public BigDecimal computeNeighbourBra(List<BigDecimal> longPath){
BigDecimal one = new BigDecimal(1);
MathContext mc = new MathContext(128,RoundingMode.HALF_UP);
int pathLength = longPath.size();
if(pathLength==1){
return longPath.get(0).add(one,mc);
}
one = one.setScale(128, RoundingMode.HALF_UP);
BigDecimal tempInd = longPath.get(pathLength-1).add(one,mc);
for(int i=pathLength-2;i>=0;i--){
tempInd = longPath.get(i).add(one.divide(tempInd, mc),mc);
}
return tempInd;
}
This is just the formula from Fig 2 (A) with x=1; Again, we pay attention to how we round the computations. For the "ket", we have:
xxxxxxxxxx
public BigDecimal computeNeighbourKet(List<BigDecimal> longPath){
MathContext mc = new MathContext(128,RoundingMode.HALF_UP);
BigDecimal eps = new BigDecimal("0.000000000000000000000000000000000000000000000000001");
eps = eps.setScale(128, RoundingMode.HALF_UP);
int pathLength = longPath.size();
if(pathLength==1){
return longPath.get(0).add(eps,mc);
}
BigDecimal one = new BigDecimal(1);
one = one.setScale(128, RoundingMode.HALF_UP);
BigDecimal tempInd = longPath.get(pathLength-1).add(eps,mc);
for(int i=pathLength-2;i>=0;i--){
tempInd = longPath.get(i).add(one.divide(tempInd, mc),mc);
}
return tempInd;
}
Here we compute the formula from Fig 2 (A) with x=inf. Notice the very small eps; it is our approximation to 1/inf value. Clearly, eps should be much smaller then pow(10,-28)- the precision of Decimal numbers in the database. Let's see how to use these "bra" and "ket" to find all descendants of an element.
The descendants of an element are found the following way:
xxxxxxxxxx
public Collection<CommentRnd> findCommentsByPathWithParent(String path) {
MathContext mc = new MathContext(128, RoundingMode.HALF_UP);
BigDecimal epsDb = new BigDecimal("0.000000000000000000000000001");
epsDb = epsDb.setScale(128, RoundingMode.HALF_UP);
Comment c = new Comment();
c.setPathString(path);
BigDecimal to = c.computeNeighbourBra();
BigDecimal from = c.computeNeighbourKet();
if(from.compareTo(to)==1) {
return comRepo.findAllChildrenByIndex(to.subtract(epsDb,mc),from.add(epsDb,mc));
}
else{
return comRepo.findAllChildrenByIndex(from.subtract(epsDb,mc),to.add(epsDb,mc) );
}
}
Here comRepo.findAllChildrenByIndex(to,from) simply swipes over all the elements, where the index is within ]to, from[ interval.
xxxxxxxxxx
public interface CommentRndRepository extends JpaRepository<CommentRnd, Long> {
( "SELECT c FROM CommentRnd c WHERE c.index >:from AND c.index <:to" )
Collection<CommentRnd> findAllChildrenByIndex(("from") BigDecimal from, ("to") BigDecimal to);
}
Notice that we have another small number here: epsDb=pow(10,-27). When the database rounds floats, only 28 digits are left, so we have no control over that margin on the edges of the interval. Also, very deep descendant comments with their indexes closer to the edges of the ancestor interval may seep out of the interval due to rounding error. For this not to happen, we pad the interval edges with extra epsDb. Next, very deep neighboring comments may seep into the interval due to rounding error. Finally, recall that the ancestor indexes may be within the interval. So, how to fix these problems and resolve collisions of the same random numbers in the paths?
To remove contaminant elements and to resolve collisions due to the same random numbers in paths, we use the following algorithm:
xxxxxxxxxx
public CommentDto filterComments(Collection<Comment> collection, Comment parent) {
if(collection.isEmpty()){
return null;
}
List<Comment> collectionL = (List) collection;
//First, we sort the input over depth
Collections.sort(collectionL,new SortByDepth());
Queue<CommentDto> commentQ = new LinkedList<>();
Deque<DepthPair> depthPairsQ = new LinkedList<>();
CommentDto parentDto = new CommentDto(parent);
commentQ.offer(parentDto);
//This variable hold the info if the parent is in the collection;
//Recall, that in our index algorithm,
// the parent is GUARANTEED to be within its bra and ket!
boolean isParentThere = false;
for(Comment tempCom : collectionL){
CommentDto cdto = new CommentDto(tempCom);
//We check if the current tempCom is in the commentQ
boolean hasParInQueue = hasParent(commentQ,cdto);
if(tempCom.getDepth()<=parent.getDepth()){
//If the parent is in the collection, we set the checker to true;
if(tempCom.getId().equals(parent.getId())){
isParentThere = true;
}
continue;
}//If there is no parent within depth<=parentDepth elements, then there is NO SUCH PARENT IN THE DB
else if(isParentThere==false){
return null;
}
else if( hasParInQueue ){
//If the tempCom is in the commentQ, we update the depth deque
updateDepthQueue(depthPairsQ,tempCom);
//...add the element to commentQ
commentQ.offer(cdto);
//...find the number of elements to remove from the commentQ
int numberCommentsToRemove = checkDepthQueue(depthPairsQ);
if(numberCommentsToRemove>0){
//...and remove them.
emptyQueueDto(commentQ,numberCommentsToRemove);
}
continue;
}
}
return parentDto;
}
The algorithm accepts a comment collection, a parent comment, and outputs the root of a CommentDto tree. Basically, for every element of the collection, we look for its parent by the parent_id and add the child references to the parent's children list. It is here that we need the Adjacency List!
Specifically, we cast the input collection to a list and sort it by depth. Secondly, we initialize auxiliary an commentQ queue and a deepPairsQ deque:
xxxxxxxxxx
private class DepthPair {
private int depth;
private int counter;
public DepthPair(int depth){
this.depth = depth;
counter = 1;
}
public void increment(){
this.counter++;
}
public int getDepth(){
return this.depth;
}
public int getCounter(){
return this.counter;
}
}
where we keep count of how many elements with the current depth are in the commentQ queue. If deepPairQ.size()>2, we retrieve the last element of the deque to find the number numberCommentsToRemove = checkDepthQueue(depthPairsQ)of CommentDtos in the commentQ to be removed from the queue. The method emptyQueue(commentQ,numberCommentsToRemove)removes these elements from thecommentQ queue. Finally, the method hasParent(commentQ,tempCom) checks if the current tempCom element has a parent in the commentQ queue. You can find the full code here. How fast this algorithm is?
To analyze the total complexity of this Continous Fraction index algorithm, we need to estimate the number of SELECT calls (finds) in the database, number of retrieves from the database, and the number of operations in the filtering procedure.
As the index field is B-tree indexed, it takes just 2 SELECTs to bracket the index interval in the table. Each SELECT takes O(log(N)) operations, where N is the total number of elements in the Comments table. Then, the database engine simply swipes all the elements in between the brackets. So, its going to be O(Log(N)+CCh(A)*R), where CCh(A) is the number of "contaminated" descendants of A, R - time to batch-retrieve found elements (per element).
This contrasts with a "WITH RECURSION"- like search, where each child element needs to be SELECTed. So, it takes O(Ch(A)*log(N)+Ch(A)*R) time (provided, parent_id field is indexed), where Ch(A) is the total number of descendants of element A.
To filter the retrieved collection, it takes O(Ch(A)*W(A)) operations, where W(A) is the maximal width of the sub-tree of A. Moreover, we can filter the collection on the browser side to reduce the load of our server. Finally, the hasParent method can be easily paralleled. This is especially helpful for root comments that have a lot of child comments.
Finally, it is interesting to compare our CFi algorithm with the Adjacency List @OneToMany annotation approach that makes Ch(A) separate SELECT calls. Clearly, its complexity is O(Ch(A)*T), where T is (usually very large) connection time. Unless, the comment A is located very deeply, CFi is still faster. According to our assumption 7, such comments are rare. So, what do we got in the end?
The Results
The collection of the following trees was fed to the filtering algorithm:
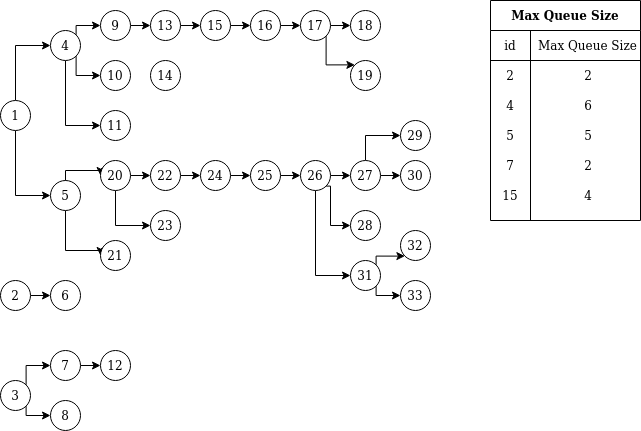
The algorithm correctly filtered all the descendants of the elements from the table. The elements are chosen to be neighbors, some are deeper than the other. Also, for every element, we filter the descendants of, the max queue size for the elements is no more then 2*max_number_of_children+1, just as it should be.
The following setup was used to test our indexing and index bracketing algorithms:
public void findAllChildIndexWithinParentBrackets(){
int M = 100;
Comment com = new Comment();
for(int K=10;K<=90;K=K+2) {
for (int j = 0; j < 100; j++) {
com.setParent(12345678L);//root id
com.setPathString("12345678");
com.setDepth(2);
for (int i = 0; i < K; i++) {
com.setPathRnd();
com.setDepth(com.getDepth() + 1);
}
BigDecimal bra = com.computeNeighbourBra();
BigDecimal ket = com.computeNeighbourKet();
for (int i = K; i <= M; i++) {
com.setPathRnd();
com.setDepth(com.getDepth() + 1);
com.computeIndex();
if (bra.compareTo(ket) == 1){ assertEquals((com.getIndex().compareTo(bra) == -1)
&& (com.getIndex().compareTo(ket) == 1), true);
} else {
assertEquals((com.getIndex().compareTo(bra) == 1)
&& (com.getIndex().compareTo(ket) == -1), true);
}
}
}
}
}
Firstly, we generate a random path to depth K, compute the bra and ket for that depth. Secondly, we keep going deeper and check if the index is within the ancestor's bra and ket. Recall that M1, M2,... numbers from our path generation algorithm? Here we set M1=99999 and Md=99 for d>2. This cycle repeats 100 times (line 6) to probe different random combinations. These tests fail at certain values K (Failure Depth in Table 1):

Here the Scale is the MathContext scale of our BigDecimals. The bigger the scale, the bigger depth the algorithm affords. We found failure depth doesn't depend much on eps=1/inf- we tested it from 30 to 70 digits, where "30" means eps=pow(10,-30). If we pad the interval with eps on both sides, the algorithm can afford bigger depth (Table 1, right).
As it is illustrated in Part 2, we choose 64 for the scale,eps=pow(10,-37), and epsDb=pow(10,-27). Indeed, if 28 is the max precision of DECIMAL number in the database, we can't store more precise numbers then this. For close very deep comments, their indexes get rounded and are equal in the database. In this case, we unravel the interwoven branches by means of the filtering algorithm.
The Conclusions
In this post, I presented a schema, an ORM entity, and a DTO for nested comments in relational databases. Also, I demonstrated how to compute index and index brackets based on continuous fractions. Finally, I showed how to filter search output and analyzed the complexity of this approach. The approach efficiently uses out of the box B-tree index, is JPQL-only, and allows full-text search over comments' content. Hope to see you in Part 2, where I will present a Spring Boot implementation of the CRUD operations.
Opinions expressed by DZone contributors are their own.

Comments