A Comprehensive Guide to Hyperparameter Tuning: Exploring Advanced Methods
Hyperparameter tuning is essential to improve model performance in machine learning. Let's delve into advanced tuning methods.
Join the DZone community and get the full member experience.
Join For FreeHyperparameter tuning is an essential practice in optimizing the performance of machine learning models. This article provides an in-depth exploration of advanced hyperparameter tuning methods, including Population-Based Training (PBT), BOHB, ASHA, TPE, Optuna, DEHB, Meta-Gradient Descent, BOSS, and SNIPER. Before delving into these methods, let's establish a foundational understanding of hyperparameters, their distinction from model parameters, and their role within the machine learning lifecycle.
What Are Hyperparameters? How Do They Differ From Model Parameters?
In the realm of machine learning, model parameters are internal variables that a model learns from training data, such as the weights and biases of a neural network. Hyperparameters, on the other hand, are external settings that govern the learning process itself. These settings are determined before training and include factors like learning rates, batch sizes, and the number of hidden layers. While model parameters adapt through training, hyperparameters remain fixed throughout the training process.
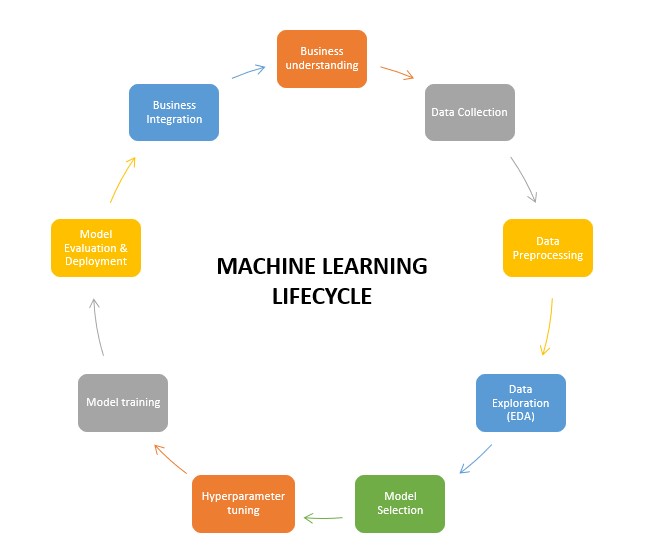
Machine Learning Lifecycle
The journey of building a machine learning model involves various stages, collectively known as the machine learning lifecycle. Hyperparameter tuning occupies a crucial position within this lifecycle. The stages typically encompass data collection, preprocessing, model selection, hyperparameter tuning, training, evaluation, and deployment.
Hyperparameter Space
Hyperparameter tuning entails navigating a multi-dimensional space, with each dimension corresponding to a specific hyperparameter. The primary challenge lies in identifying the optimal combination of hyperparameters that results in superior model performance. As the number of hyperparameters increases, manual exploration becomes infeasible. This challenge is met with the aid of advanced hyperparameter tuning methods.
Steps To Perform Hyperparameter Tuning
- Define the Hyperparameter Space: Specify the hyperparameters to be tuned and their respective value ranges.
- Choose a Performance Metric: Select a performance metric (e.g., accuracy, F1 score) to gauge the model's effectiveness.
- Select a Tuning Method: Select an appropriate hyperparameter tuning method based on the complexity of the problem and available computational resources.
- Set up a Search Strategy: Determine the strategy by which the tuning process explores the hyperparameter space. This could involve methods like random search, grid search, or more advanced techniques.
- Conduct Tuning: Execute the chosen tuning method, allowing it to explore various hyperparameter combinations.
- Evaluate Results: Assess the model's performance using the designated metric for each hyperparameter configuration.
- Select Best Configuration: Identify the hyperparameter configuration that yields the highest performance on the validation dataset.
- Test on Unseen Data: Validate the selected configuration using an unseen test dataset.
Now, let's delve into the specifics of each advanced hyperparameter tuning method, accompanied by code examples:
Population-Based Training (PBT)
Population-based training is akin to simulating an evolutionary process within the hyperparameter tuning landscape. It introduces the concept of "population," where multiple instances of a model with varying hyperparameters coexist. During training iterations, PBT evaluates the models' performances and allows the top-performing models to influence others by transferring their hyperparameters. This facilitates a dynamic balance between exploration and exploitation.
Advantages: PBT can accelerate convergence by allowing better-performing models to guide the search. It's well-suited for scenarios where different hyperparameters may shine during different stages of training.
from ray import tune
def train_model(config):
# Train the model with the given configuration
# Return the evaluation metric
tune.run(train_model, config={"lr": tune.grid_search([0.001, 0.01, 0.1]),
"batch_size": tune.grid_search([16, 32, 64])},
search_alg=tune.suggest.PopulationBasedTraining())
BOHB (Bayesian Optimization and Hyperband)
BOHB harmoniously combines the strengths of Bayesian optimization and Hyperband. Bayesian optimization creates a probabilistic model of the objective function, guiding the search for promising configurations. Hyperband efficiently allocates computational resources to different configurations, thereby optimizing the resource usage during the tuning process.
Advantages: BOHB effectively balances exploration and exploitation. It uses Bayesian optimization's modeling capabilities to guide the search efficiently, while Hyperband's resource allocation mechanism accelerates the tuning process.
from ray import tune
def train_model(config):
# Train the model with the given configuration
# Return the evaluation metric
tune.run(train_model, config={"lr": tune.uniform(0.001, 0.1),
"batch_size": tune.choice([16, 32, 64])},
search_alg=tune.suggest.BayesOptSearch(metric="metric_name"),
scheduler=tune.schedulers.HyperBandForBOHB())
ASHA (Asynchronous Successive Halving Algorithm)
Designed for distributed computing environments, ASHA enhances the successive halving algorithm by introducing asynchronous evaluations. This enables multiple configurations to be evaluated concurrently, reducing tuning time and enhancing efficiency.
Advantages: ASHA is suitable for scenarios where parallel processing capabilities are available. Its asynchronous nature minimizes idle time and speeds up the search process significantly.
from ray import tune
def train_model(config):
# Train the model with the given configuration
# Return the evaluation metric
tune.run(train_model, config={"lr": tune.uniform(0.001, 0.1),
"batch_size": tune.choice([16, 32, 64])},
search_alg=tune.suggest.ASHASearch(metric="metric_name"))
TPE (Tree-Structured Parzen Estimator)
Tree-structured Parzen Estimator constructs probabilistic models of the objective function using Bayesian inference. It intelligently explores the hyperparameter space by focusing on regions that are more likely to yield better results.
Advantages: TPE is efficient and well-suited for high-dimensional spaces. It strikes a balance between exploration and exploitation by guiding the search toward potentially promising areas.
from hyperopt import fmin, tpe, hp
def objective(params):
# Train the model with the given configuration
# Return the negative of the evaluation metric as Hyperopt minimizes
space = {"lr": hp.uniform("lr", 0.001, 0.1),
"batch_size": hp.choice("batch_size", [16, 32, 64])}
best = fmin(fn=objective, space=space, algo=tpe.suggest, max_evals=100)
Optuna
Optuna is a versatile hyperparameter optimization framework that supports various optimization algorithms, including TPE and random search. It automates the process of exploring hyperparameter configurations and refining them over trials.
Advantages: Optuna's versatility allows practitioners to experiment with multiple optimization strategies within a unified framework. It abstracts the optimization process, making it accessible and efficient.
import optuna
def objective(trial):
# Train the model with the given configuration
# Return the evaluation metric
study = optuna.create_study(direction="maximize")
study.optimize(objective, n_trials=100)
DEHB (Distributed Evolutionary Hyperparameter Tuning)
DEHB employs evolutionary algorithms to optimize hyperparameters. It manages a population of configurations and adapts their distribution over time based on their performance, creating a dynamic tuning process.
Advantages: DEHB dynamically adapts the search space and can effectively handle complex optimization landscapes. Its evolutionary approach can lead to insightful and efficient tuning.
from dehb import DEHB
def train_model(config):
# Train the model with the given configuration
# Return the evaluation metric
dehb = DEHB(min_budget=1, max_budget=10, eta=3)
results = dehb.minimize(train_model, configs_space)
Meta-Gradient Descent
Meta-Gradient Descent goes beyond traditional hyperparameter tuning by optimizing the learning rates themselves. It employs gradient information computed during training to adapt the learning rates over time.
Advantages: Meta-Gradient Descent is particularly useful for scenarios where learning rates significantly impact training convergence. It adapts the learning rates based on empirical evidence from the training process.
import torch
from torch.optim import SGD
def train_model(config):
optimizer = SGD(model.parameters(), lr=config["lr"])
for epoch in range(num_epochs):
# Training loop
model = ... # Initialize your model
config = {"lr": 0.01}
for meta_iteration in range(num_meta_iterations):
optimizer = MetaOptimizer(config["lr"])
train_model(config)
config["lr"] = optimizer.get_updated_lr()
BOSS (Bayesian Optimization With Structure Sampling)
BOSS enhances Bayesian optimization by incorporating structured kernels, which capture relationships between hyperparameters. This accelerates convergence by leveraging the inherent structure within the data.
Advantages: BOSS is effective when the hyperparameters exhibit complex interactions. It leverages structured kernels to efficiently explore the hyperparameter space and discover promising configurations.
from bayesian_optimization_structure_sampling import BOSS
def objective(params):
# Train the model with the given configuration
# Return the evaluation metric
space = {"lr": (0.001, 0.1),
"batch_size": (16, 64)}
boss = BOSS(objective, space, structure="kernel_matrix")
results = boss.optimize(n_iter=100)
SNIPER (Scalable and Noise-Invariant Parallel Optimization)
SNIPER addresses challenges in parallel hyperparameter tuning, such as noisy evaluations and resource constraints. It intelligently allocates resources to configurations based on their past evaluations, ensuring efficient exploration.
Advantages: SNIPER is designed for noisy environments and can manage resource allocation effectively. It adapts to the varying qualities of evaluations and prevents the over-allocation of resources to unpromising configurations.
from sniper import SNIPER
def train_model(config):
# Train the model with the given configuration
# Return the evaluation metric
sniper = SNIPER(objective=train_model, n_workers=4)
best_config = sniper.run()
Conclusion
In the rapidly evolving landscape of machine learning, achieving the best model performance is vital, which demands not only using innovative algorithms and cutting-edge architectures but also a deep understanding of hyperparameter tuning. As models become more intricate and datasets grow in complexity, the significance of optimizing hyperparameters becomes increasingly pronounced. This article has elucidated how advanced hyperparameter tuning methods serve as indispensable allies in the quest for optimal model performance.
In my next articles, I will delve into each of the hyperparameter tuning methods discussed above, providing detailed explanations and insights for a comprehensive understanding of their applications.
Do you have any questions related to this article? Leave a comment and ask your question, and I will do my best to answer it.
Thanks for reading!
Opinions expressed by DZone contributors are their own.

Comments