The What, When, and Why of Regularization in Machine Learning
Learn more about regularization in machine learning.
Join the DZone community and get the full member experience.
Join For FreeIn this post, we will try and understand some of the following in relation to regularizing the regression of machine learning models to achieve higher accuracy and stable models:
- Background
- What is regularization?
- Why and when does one need to adopt/apply the regularization technique?
Background
At times, when you are building a multi-linear regression model, you use the least-squares method for estimating the coefficients of determination or parameters for features. As a result, some of the following happens:
Often, the regression model fails to generalize on unseen data. This could happen when the model tries to accommodate all kinds of changes in the data including those belonging to both the actual pattern and also the noise. As a result, the model ends up becoming a complex model having significantly high variance due to overfitting, thereby impacting the model performance (accuracy, precision, recall, etc.) on unseen data. The diagram below represents the high variance regression model.

The goal is to reduce the variance while making sure that the model does not become biased (underfitting). After applying the regularization technique, the following model could be obtained.
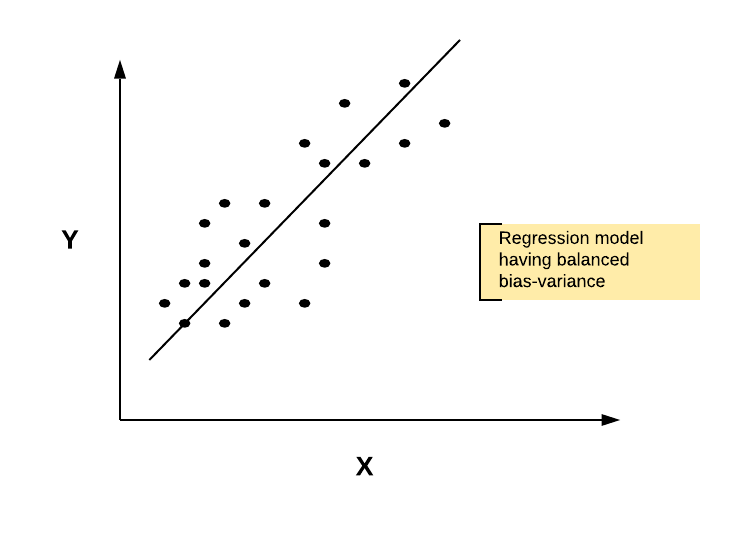 Fig 2. The regression model after regularization is applied
Fig 2. The regression model after regularization is applied
- A large number of features and the related coefficients (at times large enough) result in computationally intensive models.
The above problems could be tackled using regularization techniques which are described in later sections.
What Is Regularization?
Regularization techniques are used to calibrate the coefficients of the determination of multi-linear regression models in order to minimize the adjusted loss function (a component added to the least-squares method). Primarily, the idea is that the loss of the regression model is compensated using the penalty calculated as a function of adjusting coefficients based on different regularization techniques.
Adjusted loss function = Residual Sum of Squares + F(w1, w2, …, wn) …(1)
In the above equation, the function denoted using “F” is a function of weights (coefficients of determination).
Thus, if the linear regression model is calculated as the following:
Y = w1*x1 + w2*x2 + w3*x3 + bias …(2)
The above model could be regularized using the following function:
Adjusted Loss Function = Residual Sum of Squares (RSS) + F(w1, w2, w3) …(3)
In the above function, the coefficients of determination will be estimated by minimizing the adjusted loss function instead of simply RSS function.
In later sections, you will learn about why and when regularization techniques are needed/used. There are three different types of regularization techniques. They are as following:
- Ridge regression (L2 norm)
- Lasso regression (L1 norm)
- Elastic net regression
For different types of regularization techniques as mentioned above, the following function, as shown in equation (1), will differ:
F(w1, w2, w3, …., wn)
In later posts, I will be describing different types of regression mentioned above. The difference lies in the adjusted loss function to accommodate the coefficients of parameters.
Why Do You Need to Apply a Regularization Technique?
Often, the linear regression model comprising of a large number of features suffers from some of the following:
- Overfitting: Overfitting results in the model failing to generalize on the unseen dataset
- Multicollinearity: Model suffering from multicollinearity effect
- Computationally Intensive: A model becomes computationally intensive
The above problem makes it difficult to come up with a model which has higher accuracy on unseen data and which is stable enough.
In order to take care of the above problems, one goes for adopting or applying one of the regularization techniques.
When Do You Need to Apply Regularization Techniques?
Once the regression model is built and one of the following symptoms happen, you could apply one of the regularization techniques.
- Model lack of generalization: Model found with higher accuracy fails to generalize on unseen or new data.
- Model instability: Different regression models can be created with different accuracies. It becomes difficult to select one of them.
References
Summary
In this post, you learned about the regularization techniques and why and when are they applied. Primarily, if you have come across the scenario that your regression models are failing to generalize on unseen or new data or the regression model is computationally intensive, you may try and apply regularization techniques. Applying regularization techniques make sure that unimportant features are dropped (leading to a reduction of overfitting) and also, multicollinearity is reduced.
Published at DZone with permission of Ajitesh Kumar, DZone MVB. See the original article here.
Opinions expressed by DZone contributors are their own.

Comments