The Equivalence Rationale of Neural Networks and Decision Trees: Towards Improving the Explainability and Transparency of Neural Networks

Over the past decade, neural networks have succeeded immensely in various industries. However, the black-box nature of their predictions has prevented their broader and more reliable adoption in fields such as health and security. This has led researchers to investigate ways to explain neural network decisions. 

One approach to explaining neural network decisions is through saliency maps, which highlight areas of the input that a neural network uses most while making a prediction. However, these methods often produce noisy results that do not clearly understand the decisions made. 

Another track of methods involves the conversion of neural networks to interpretable-by-design models, such as decision trees. This conversion has been a topic of interest for researchers, but most existing methods need more generalization to any model or provide only an approximation of a neural network.

In this blog, we unravel a new approach to improving the explainability and transparency of neural networks. We show that an equivalent decision tree can directly represent any neural network without altering the neural architecture. The decision tree representation provides a better understanding of neural networks. Furthermore, it allows for analyzing the categories a test sample belongs to, which can be extracted by the node rules that categorize the sample.

Our approach extends previous works' findings and applies to any activation function and recurrent neural networks. This equivalence rationale of neural networks and decision trees has the potential to revolutionize the way we understand and interpret neural networks, making them more transparent and explainable. Furthermore, we show that the decision tree equivalent of a neural network is computationally advantageous at the expense of increased storage memory. In this blog, we will explore the implications of this approach and discuss how it could improve the explainability and transparency of neural networks, paving the way for their wider and more reliable adoption in critical fields such as health and security. 

Extending Decision Tree Equivalence to Any Neural Network with Any Activation Function

The feedforward neural networks with piece-wise linear activation functions such as ReLU and Leaky ReLU are crucial and lay the foundation for extending the decision tree equivalence to any neural network with any activation function. In this section, we will explore how the same approach can be applied to recurrent neural networks and how the decision tree equivalence also holds for them. We will also discuss the advantages and limitations of our approach and how it compares to other methods for improving the interpretability and transparency of neural networks. Finally, let's dive into the details and see how this extension can be achieved.

Utilizing Fully Connected Networks

In equation 1, we can represent a feedforward neural network's output and intermediate feature given an input x0, where Wi is the weight matrix of the network's ith layer, and σ is any piece-wise linear activation function. This representation is crucial in deriving the decision tree equivalence for feedforward neural networks with piece-wise linear activation functions. By using this representation, we can easily extend the approach to any neural network with any activation function, as we will see in the next section.

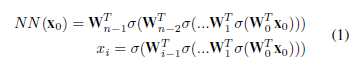
Equation 1 represents a feedforward neural network's output and intermediate feature, but it omits the final activation and bias term. The bias term can be easily included by adding a 1 value to each xi. Additionally, the activation function σ acts as an element-wise scalar multiplication, which can be expressed as shown.

Equation 2 represents the vector ai-1, which indicates the slopes of activations in the corresponding linear regions where W^T_i-1 and x_i-1 fall into, and ⊙ denotes element-wise multiplication. This vector can be interpreted as a categorization result since it includes indicators (slopes) of linear regions in the activation function. By reorganizing Eq. 2, we can further derive the decision tree equivalence for any neural network with any activation function, as we will see in the next section.

Equation 3 uses ⊙ as a column-wise element-wise multiplication on Wi, which corresponds to element-wise multiplication by a matrix obtained by repeating a_i-1 column-vector to match the size of Wi. By using Eq. 3, we can rewrite Eq. 1 as follows.

Eq. 4 defines an effective weight matrix Ŵ^T_i of a layer i to be applied directly on input x₀, as shown below.

In Eq. 5, we can observe that the effective matrix of layer i only depends on the categorization vectors from previous layers. This means that in each layer, a new efficient filter is selected to be applied to the network input based on the previous categorizations or decisions. This demonstrates that a fully connected neural network can be represented as a single decision tree, where effective matrices act as categorization rules. This approach greatly improves the interpretability and transparency of neural networks and can be extended to any neural network with any activation function.

Equation 5 Can Be Deduced From the Following Algorithms:

Normalization layers do not require a separate analysis, as popular normalization layers are linear. After training, they can be embedded into the linear layer after or before pre-activation or post-activation normalizations, respectively. This means that normalization layers can be incorporated into the decision tree equivalence for any neural network with any activation function without additional analysis.

Moreover, effective convolutions in a neural network are only dependent on categorizations coming from activations, which enables the tree equivalence similar to the analysis for fully connected networks. However, a difference from the fully connected layer case is that many decisions are made on partial input regions rather than the entire x0. This means that the decision tree equivalence approach can be extended to convolutional neural networks but with the consideration of the partial input regions. By incorporating normalization layers and convolutional layers, we can create a decision tree that captures the entire neural network, significantly improving interpretability and transparency.

In Equation 2, the possible values of the elements in 'a' are limited by the piece-wise linear regions in the activation function for piece-wise linear activations. The number of these values determines the number of child nodes per effective filter. When using continuous activation functions, the number of child nodes becomes infinite width for even a single filter because continuous functions can be thought of as having an infinite number of piece-wise linear regions. Although this may not be practical, we are mentioning it for completeness. To prevent infinite trees, one option is to use quantized versions of continuous activations, which will result in only a few piece-wise linear regions and, therefore, fewer child nodes per activation.

As recurrent neural networks (RNNs) can be transformed into a feedforward representation, they can also be represented as decision trees in a similar way. However, the particular RNN being studied in this case does not include bias terms, which can be defined by adding a 1 value to input vectors.

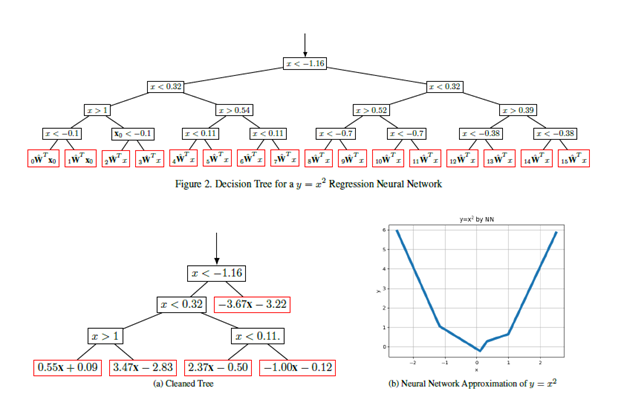
Cleaned Decision Tree for a y = x2 Regression Neural Network

Conclusion

In conclusion, building on existing research is crucial in advancing the field of neural networks, but it is equally essential to avoid plagiarism. 

The equivalence between neural networks and decision trees has significant implications for improving the explainability and transparency of neural networks. By representing neural networks as decision trees, we can gain insights into the inner workings of these complex systems and develop more transparent and interpretable models. This can lead to greater trust and acceptance of neural networks in various applications, from healthcare to finance to autonomous systems. While challenges remain in fully understanding the complex nature of neural networks, the tree equivalence provides a valuable framework for advancing the field and addressing the black-box problem. As research in this area continues, we look forward to discoveries and innovations that will drive the development of more interpretable and explainable neural networks.

By understanding the tree equivalence of neural networks, we can gain insight into their inner workings and make more informed decisions in designing and optimizing them. This knowledge can help us address the challenge of interpreting the black-box nature of neural networks. So, let's continue to explore the fascinating world of neural networks with a curious and creative spirit.