The Developer's Guide to Collections: Queues
Let's continue our journey into Java collections by examining the concept and proper usage of queues and deques in your code.
Join the DZone community and get the full member experience.
Join For FreeQueues are an essential part of most software applications, whether in an isolated system or a widely-distributed, networked application. In recent years, queues have taken on an entirely new meaning with the acceptance of the Advanced Message Queuing Protocol (AMQP) and many of its implementations, such as RabbitMQ. While these are important aspects of the Java ecosystem, the same importance of queues can be found at the micro-application level, as well. For example, many concurrent (multi-threaded) applications require queues to process data or execute tasks. This category of problem is so prolific, it has even been codified into a well-known problem for decades: The Producer-Consumer problem.
In this last installment of The Developer's Guide to Collections, we will export the queue portion of the Java Collections Framework (JCF) and focus particularly on two types of data structures: Queues and double-ended queues (deque; pronounced "deck"). Starting with an explanation of the concepts behind queues, we will work our way into the actual code of the Queue and Deque interfaces, looking at the intent and logic behind each of these abstractions of the queue concept. Lastly, we will delve into the various queue implementations Java offers and how each implementation differs from one another. With this understanding, we will then be able to make grounded decisions about when and when not to use each implementation. Before diving into these details, though, we must first gain a solid grasp of the concept of a queue.
The Concept of a Queue
A queue is one of the most familiar of collections we see on a daily basis. When we check out at a supermarket, we form a queue at the register (some British dialects refer to this as queuing). Likewise, when we travel through a drive-through window at a fast food restaurant, we insert our car in a line of other cars and the restaurant staff handles orders one car at a time, starting with the first car in the line and terminating with the last car in the line. Although seemingly different in their application, each of these concepts is closely related. In general, a queue can be defined as follows:
A queue is a collection of elements to be processed
Queues have a distinct set of characteristics and behaviors, where the insertion of a new element in a queue is called enqueuing and the atomic retrieval and removal of the next element from the queue is called dequeuing. If we wish to retrieve the next element from a queue without removing it from the queue, we can peek at the queue, which results in the next element from the queue but leaves it in the queue. Although not all queues are formed in the same manner, the most common type of queue (such as in the supermarket or drive-through examples) is the First-in-First-out (FIFO) queue.
FIFO Queues
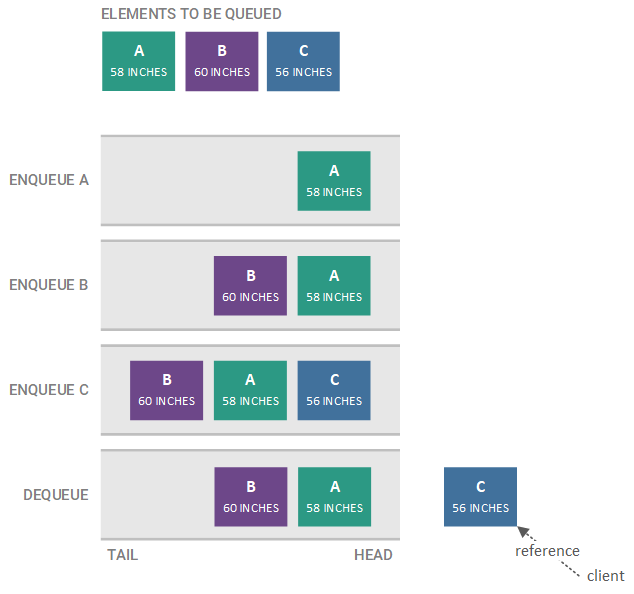
The order of the elements in a queue can vary by the type of queue. In most cases, though, queues are FIFO queues, where the first element enqueued is the first element dequeued. For example, if we enqueue elements A, B, and C (in that order) on a queue, the next element to be dequeued is A, since it is was the first element enqueued (i.e. it is the oldest element). In general, the next element to be dequeued from a queue (in this case, A) is called the head of the queue. A FIFO queue is illustrated in the figure below.

The example of the A, B, and C elements being added to a FIFO queue is illustrated in the figure below. Each enqueue and dequeue step, along with the resulting state of the FIFO queue, is shown, starting with the topmost step and ending with the bottom-most step.
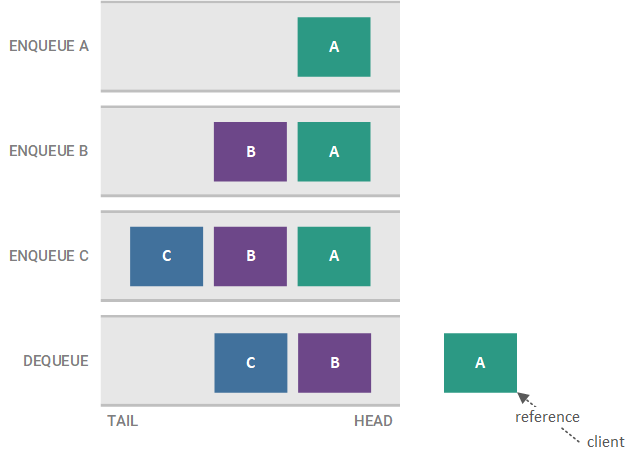
Note that we do not dequeue a specific element (i.e. we do not say dequeue A). Instead, the head of the queue is always returned when we dequeue; therefore, the target of the dequeue is always implicitly the head of the queue and is never explicitly specified.
Stacks
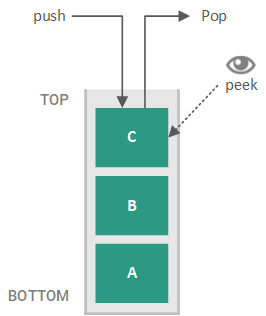
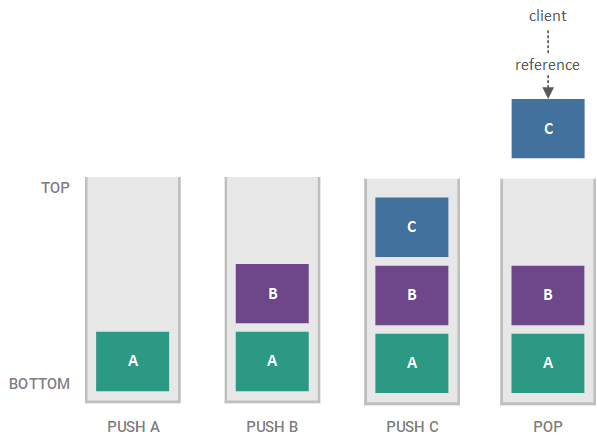
The counterpart to a FIFO queue is a Last-in-First-out (LIFO) queue, or a stack, where the last element to be enqueued is the next element to be dequeued. In the vernacular of stacks, the position of the last element pushed onto the stack is called the top and the position of the first element pushed onto the stack is called the bottom (stacks are usually illustrated vertically, such as seen with stacks of paper to be processed or stacks of dishes to be cleaned). For example, if we enqueue elements A, B, and C (in that order) on a stack, the next element to be dequeued is C. With stacks, enqueuing an element is called pushing an element onto the stack while dequeuing an element is called popping an element off of the stack. A stack is illustrated in the figure below.
The previous example of our stack, using A, B, and C as elements, is illustrated in the figure below, with each successive horizontal pane representing the state of the stack as elements are pushed onto it or popped from it.
Similar to the FIFO queue, we do not specify the target of the pop operation on a stack (i.e. we do not say pop C). Instead, the pop operation always has an implicit target of the top of the stack and thus, no explicit target is provided.
Priority Queues
Although both the FIFO queues and stacks both enqueue from one or the other end (i.e. tail for FIFO queues and the top for stacks), there are queues that may enqueue elements at any interior position as well. For example, if we queued patients at a hospital, we would want to enqueue elements by the severity of each patient's injury, rather than when the patient arrived at the hospital. This particular queue is called a priority queue, where each element is assigned a priority and enqueued according to this priority.
The priority of each element may not necessarily be an absolute priority (such as in hospital triage, where an immediate patient always has a higher priority than minimal), but rather, may have a relative priority. For example, when children are lined up in a classroom by height order, a relative priority is used: Each student is added to the line such as he or she is taller than the student in front and shorter than the student behind him or her. Separate from the group, each student is not considered short or tall, but rather, is considered shorter or taller than another student. In essence, we can discover if a priority is absolute or relative based on the use of superlative or comparative adjectives, respectively (i.e. the most immediate patient for absolute priority or the taller student for relative priority).
The concept of a priority queue is illustrated in the figure below (where 0 is the highest priority and 2 is the lowest priority).
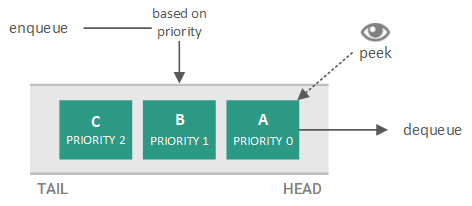
A priority queue based on the previously discussed classroom lineup scheme is illustrated in the figure below (where the shortest students are placed at the "head of the line").
Double-Ended Queues
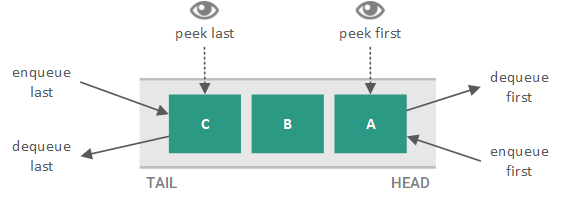
In the queues we have already seen, elements are always dequeued from the head (or top) of the queue, regardless of the location in which they were enqueued. In general, these types of queues are called single-ended queues since only one end of the queue can be dequeued. In contrast, there are queues from which either end of the queue can be accessed. These double-ended queues (called deques, pronounced decks) can enqueue and dequeue elements from either end. One end of the queue is called the head, where the element at the head of the queue is called the first element, and the other end is called the tail, where the element at the tail of the queue is called the last element.
It is important to note that all of the queuing behaviors (enqueuing, dequeuing, and peeking) can be used at either end of the deque. This results in six behaviors:
- Enqueue at head
- Dequeue at head
- Peek at head
- Enqueue at tail
- Dequeue at tail
- Peek at tail
The concept of a deque is illustrated in the figure below.
Deques can conceptually be thought of as the most general of queues, where each of the previously discussed queue types can be theoretically represented by a deque:
- FIFO queue: A deque where elements are enqueued at the tail and dequeued at the head
- Stack: A dequeue where elements are enqueued and dequeued at the head
- Priority queue: A dequeue where elements are enqueued according to their absolute or relative priority and are dequeued at the head
With the concept of a queue, as well as their specializations, under our belt, we can now explore the Queue interface, along with Deque interface, that make up the JCF implementation of the general queuing concepts.
The Queue Interfaces
Although most off-springs of the Collection interface have a primary sub-interface for their hierarchies (e.g. List and Set interfaces), the queue portion of the collection framework has two: (1) the Queue interface and (2) the Deque interface. Although the Deque interface is actually a sub-interface of the Queue interface, it is important enough to discuss it distinctly from its parent interface.
Queue
The Queue interface is a simple interface that captures the basic behavior of a theoretical queue. The Java Development Kit (JDK) 9 interface specification for the Queue interface is depicted in the following snippet.
public interface Queue<E> extends Collection<E> {
boolean add(E e);
boolean offer(E e);
E remove();
E poll();
E element();
E peek();
}The methods of the Queue interface can be divided into two categories: Those that throw exceptions to denote failed operations and those that return special values to denote failed operations. The add and offer methods are identical, enqueuing the supplied element to the queue, but the former throws an IllegalStateException if the element cannot be added due to the state of the queue while the latter returns false if the element cannot be added. Likewise, the remove method throws a NoSuchElementException if the there is no element to dequeue and the poll method returns null if there is no element to dequeue. Lastly, the element method peeks at the head of the queue, throwing a NoSuchElementException if there is no element at the head of the queue while the peek method returns null if no head exists. In general, the special-return-value methods should be used if failure to enqueue, dequeue, or peek is common or expected, such as when using a bounded queue.
In general, the Queue interface methods can be summed up as follows:
| Queue Operation | Exception-Throwing Method | Special-Return Method |
| enqueue | add |
offer |
| dequeue | remove |
poll |
| peek | element |
peek |
add(E e) and offer(E e)
Both methods enqueue the element, e, to the queue and return true if the supplied element was successfully added. If the queue implementation does not have a large enough capacity to enqueue the supplied element, the add method throws an IllegalStateException while the offer method returns false. For queue implementations with a non-trivial capacity restriction (i.e. a bounded queue), clients should prefer offer over add.
remove and poll
Both methods dequeue the head of the queue and return the dequeued element (the previous head) of the queue. If no head exists (i.e. the queue is empty), the remove method will throw a NoSuchElementException while the poll method will return null.
element and peek
Both methods peek at the head of the queue and non-destructively return the current head of the queue (does not remove the head). If no head exists (i.e. the queue is empty), the element method throws a NoSuchElementException while the peek method returns null.
Deque
The interface for a deque may appear to be much more complicated than that of the standard Queue interface, but upon further examination, it is actually quite simple. The JDK 9 Deque interface is depicted in the listing below.
public interface Deque<E> extends Queue<E> {
void addFirst(E e);
void addLast(E e);
boolean offerFirst(E e);
boolean offerLast(E e);
E removeFirst();
E removeLast();
E pollFirst();
E pollLast();
E getFirst();
E getLast();
E peekFirst();
E peekLast();
boolean removeFirstOccurrence(Object o);
boolean removeLastOccurrence(Object o);
boolean add(E e);
boolean offer(E e);
E remove();
E poll();
E element();
E peek();
boolean addAll(Collection<? extends E> c);
void push(E e);
E pop();
boolean remove(Object o);
boolean contains(Object o);
int size();
Iterator<E> iterator();
Iterator<E> descendingIterator();
}Although this interface includes many more methods that the Queue interface, it only does so because all of the operations of the Queue interface can be executed on either side (head or tail) of the deque. For example, in the case of a Queue, we can only enqueue an element at one side of the queue, but with a Deque, we can enqueue elements at the front (head) or the back (tail). Thus, we only have the add and offer methods for the Queue interface, but we have the addFirst, addLast, offerFirst, and offerLast methods for the Deque interface.
The Enqueue, Dequeue, and Peek Methods
In general, the following enqueue, dequeue, and peek methods are enumerated for a Deque:
| OPERATION | End | EXCEPTION METHOD | SPECIAL-RETURN METHOD |
| enqueue | Front | addFirst |
offerFirst |
| Back | addLast |
offerLast |
|
| dequeue | Front | removeFirst |
pollFirst |
| Back | removeLast |
pollLast |
|
| peek | Front | getFirst |
peekFirst |
| Back | getLast |
peekLast |
Note that while the Queue interface has the element method, the Deque interface uses getter methods in its place (instead of elementFirst and elementLast, the Deque interface uses getFirst and getLast, respectively). In the same manner as the Queue interface, the add, remove , and get methods throw exceptions when the desired operation cannot be performed (the same exceptions as their Queue interface counterparts), while the offer, poll, and peek methods use special return values to denote failure of the desired operation.
removeFirstOccurrence(Object o), removeLastOccurrence(Object o), and remove(Object o)
The first two methods act as convenience methods, removing the first element that matches the supplied element and the last element that matches the supplied element, respectively, from the deque. Matching elements are determined using the Object#equals method, which uses the following logic for each element, e, in the deque: (o == e) || (o != null && o.equals(e)). In both cases, true is returned if the supplied element was removed from the deque.
The remove method is logically equivalent to the removeFirstOccurrence method, removing the first matching element in the deque and returning true if the a matching element was successfully removed from the deque.
The Queue Interface Methods
Since the deques are also queues, the Deque interface extends the Queue interface and expects the methods inherited from the Queue interface to behave as FIFO operations. Thus, calling addor offer enqueues an element to the tail of the queue; calling remove or poll dequeues an element from the head of the queue; calling element or peek peeks at the element at the head of the queue. Thus, the existing Queuemethods can be summarized as equivalent Deque interface behaviors in the following table (note that this does not mean that a Deque implementation must call these methods, but rather, these methods have equivalent behavior):
| QUEUE Method | Deque Method |
| add | addLast |
| offer | offerLast |
| remove | removeFirst |
| poll | pollFirst |
| element | getFirst |
| peek | peekFirst |
addAll(Collection<? extends E> c)
This method enqueues all of the elements in the supplied collection to the tail of deque. This method is equivalent to calling addLast for each element and returns true if deque changed as a result of this call. If a deque implementation has a non-trivial capacity restriction, it is preferable to call offer on each of the element in c rather than calling addAll.
push(E e) and pop
As stated in the conceptual overview section of this article, deques can also be used as stacks. Thus, the Deque interface includes stack methods–namely push and pop (as peek already exists). Although a Stack interface does not exist in the collections framework (as there already exists a Stack class in the framework), it can be effectively understood to be the following (note that this interface does not exist in the collections framework):
public interface Stack<E> {
void push(E e);
E pop();
E peek();
}Although the Stack interface does not exist, the Deque interface includes these methods as though they did and expects the behavior of these methods to reflect the following Deque methods:
| QUEUE METHOD | DEQUE METHOD |
| push | addFirst |
| pop | removeFirst |
| peek | peekFirst |
Note that the push and pop methods use the exception-throwing style methods while the peek method uses the special-return-value style method.
contains(Object o) and size
The contains method returns true if the supplied object is contained in the deque and returns false otherwise. The size method returns the current number of elements in the deque.
iterator and descendingIterator
The iterator method returns an Iterator that will traverse each element of the deque sequentially starting at its head (first element) and ending with its tail (last element). The descendingIterator returns an Iterator that traverses the deque in the reverse order, starting at the tail (last element) and ending with the head (first element).
The Queue Hierarchy
The Queue interface hierarchy may appear more complicated than other collection subtype hierarchies, but if we keep our wits about the conceptual idea of a queue, it is actually quite simple. The non-concurrent hierarchy for the JDK 9 Queue interface is illustrated below, where interfaces are represented in green, abstract classes are represented in blue, and concrete implementation classes are represented in purple.
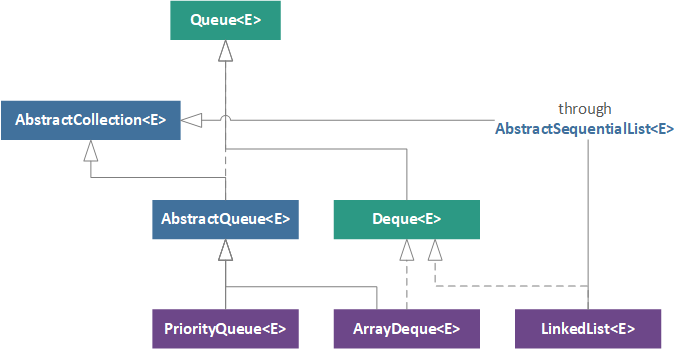
Starting with the root of the interface, we reach the Queue interface, which defines the basic queue behaviors (enqueuing, dequeuing, and peeking) as seen in the previous section. Following the left side of the hierarchy down, we reach the AbstractQueue class, which is a more specialized AbstractCollection class that maintains the basic queue functionality for add, remove, element, and addAll in terms of its special-return-value methods. At the bottom of the hierarchy, we reach the PriorityQueue class, which represents the only implementation class in this hierarchy that is solely a Queue (and not a Deque as well).
Moving to the right, we reach the Deque interface, which contains the methods necessary for a deque (as seen in the previous section) and its immediate implementation, the ArrayDeque. Lastly, we have the LinkedList implementation class, which we saw in The Developer's Guide to Collections: Lists article, but this time, we see that it also represents a deque. Although this may seem strange to have a List representing a deque, if we peer into the implementation of the LinkedList class, we see that this relationship is straightforward. LinkedList is simply a bidirectional linked list implementation, which means that elements can be easily added to the head or the tail of a LinkedList.
This is nearly identical to the functionality of a deque, where elements are enqueued and dequeued from the front (head) and back (tail) of the deque. This similarity is so apparent that the concrete implementation of the Deque interface methods (such as addFirst) are trivially implemented using the existing LinkedList methods. For example, addFirst directly delegates (one-to-one) to the private linkFirst method, which links a given element to the first position of the LinkedList (i.e. a simple linking to the head of the LinkedList).
With a fundamental understanding of the Queue hierarchy, we will look at each of the implementation classes in the following sections, focusing on the varying performance characteristics of each and which use cases each is best suited for.
PriorityQueue
This implementation class is an unbounded queue that uses a priority heap as its internal data structure (does not support null elements). Due to its heap implementation, its enqueue, dequeue, and peek operations have the following performance characteristics (see Stackoverflow and Comparing Queue Implementations):
- add(E e) & offer(E e): O(log(n))
- remove & poll: O(log(n))
- element & peek: O(1)
- contains: O(n)
- size: O(1)
Apart from its performance characteristics, the PriorityQueue class is ideal for queues that require ordering through an explicit Comparator object or whose elements have some natural ordering. For example, if an application is processing a set of tasks with some inherent priority, a PriorityQueue can be used to ensure that when elements are dequeued and processed, they are processed according to their associated priority, as illustrated in the snippet below (where 0 represents the highest priority and sequentially increasing integers represent gradually decreasing priorities):
public class Task implements Comparable<Task> {
private final int priority;
public Task(int priority) {
this.priority = priority;
}
public int getPriority() {
return priority;
}
@Override
public int compareTo(Task other) {
return this.priority - other.priority;
}
@Override
public String toString() {
return "Task[priority=" + priority + "]";
}
}
Queue<Task> tasks = new PriorityQueue<>();
tasks.add(new Task(1));
tasks.add(new Task(2));
tasks.add(new Task(0));
while (tasks.size() > 0) {
System.out.println("Processed: " + tasks.poll());
}This example uses natural ordering, where the Task class implements the Comparable<Task> interface, ensuring that one Task object is comparable to another. Due to the fact that the priorities are low for this example (and overflow from subtraction of priorities is unlikely), we use the integer comparison idiom, where the other value is subtracted from the current value, which results in a zero if the two are equal, negative value if the other value is greater (negative value denoting a higher priority), and positive value if the current priority is greater than the other priority (positive value denoting a lower priority). If we execute this snippet, we see the following:
Processed: Task[priority=0]
Processed: Task[priority=1]
Processed: Task[priority=2]We could also use an explicit Comparator<Task> object to achieve the same results:
public class TaskComparator implements Comparator<Task> {
@Override
public int compare(Task task1, Task task2) {
return task1.getPriority() - task2.getPriority();
}
}
public class Task {
private final int priority;
public Task(int priority) {
this.priority = priority;
}
public int getPriority() {
return priority;
}
@Override
public String toString() {
return "Task[priority=" + priority + "]";
}
}
Queue<Task> tasks = new PriorityQueue<>(new TaskComparator());
tasks.add(new Task(1));
tasks.add(new Task(2));
tasks.add(new Task(0));
while (tasks.size() > 0) {
System.out.println("Processed: " + tasks.poll());
}Note that if we do not supply a Comparator object to the PriorityQueue constructor, the add method throws a ClassCastException. By default, if no explicit Comparator object is supplied to the PriorityQueue constructor, the PriorityQueue attempts to use natural ordering (which requires that its element, of type E, implement the Comparable<E> interface) to order its element. Since we did not provide such an object to the constructor or provide elements that implement the Comparable interface, the PriorityQueue is incapable of properly ordering its elements.
ArrayDeque
This implementation uses a resizable array to support an unbounded number of elements. This implementation is analogous to the ArrayList implementation for the List interface, where the underlying array is given an initial capacity and must grow when its capacity is insufficient to support the number of elements enqueued. Due to its array-based implementation, all major operations execute in constant time (see Comparing Queue Implementations and the official ArrayDeque documentation):
- add(E e) & offer(E e): O(1)
- poll: O(1)
- remove: O(n)
- element & peek: O(1)
- contains: O(n)
- size: O(1)
In general, this implementation is faster than the Stack class when used as a stack and faster than the LinkedList when used as a queue.
LinkedList
This implementation is covered in depth in The Developer's Guide to Collections: Lists. Although we will not reiterate a detailed discussion of this class when using this class as a queue, it has the following complexities for its Queue interface methods:
- add(E e) & offer(E e): O(1)
- poll & remove: O(1)
- element & peek: O(1)
- contains: O(n)
- size: O(1)
Compared to the ArrayDeque, this implementation is well suited for interior removal. For example, when removing an element during iteration (from the interior of the deque), the linked list implementation does not need to patch the fragmentation in its underlying array; instead, it simply changes the next and previous references, healing the internal fragmentation in constant time. In general, unless removal of interior elements is required, an ArrayDeque should be used.
Comparison
The following table summarizes the advantages and disadvantages of each Queue interface implementation, including when each implementation is best suited for use:
| Queue | Description |
PriorityQueue |
A queue implementation best used when the elements of the queue have inherent priority, such as tasks with an associated priority or children who are to be lined up in height order. This implementation has O(log(n)) complexity for its enqueue, dequeue, and search (contains) methods and while its peek and size methods execute in constant time. This implementation should be favored only when Comparable objects are used as elements or an explicit Comparator object is needed to impose ordering of elements. |
ArrayDeque |
A generally well-performing implementation that executes its methods in constant time (except for remove and contains). This implementation should be used as a default except in the specific cases enumerated in the other two implementations. |
LinkedList |
A linked list implementation of a deque that is better suited when interior removal is required (such as removing elements while iterating over the deque). In general, an ArrayDeque should be preferred over this implementation. |
Conclusion
Queues are an essential part of most Java applications, at both the macro as well as micro level. These data structures are so important that the JCF includes its own implementations for queues, as well as specializations of this concept in the form of deques and priority queues. While a cursory overview of this series of interfaces and classes suffices to understand the basics of queues in Java, we as developers need to go deeper, exploring the fine details of each interface and class, understanding both its intent and its uses. Not only will this aid in the creation of better software, it will also drive us to write software that better fits the original intent of the JCF.
If you enjoyed this article and want to learn more about Java Collections, check out this collection of tutorials and articles on all things Java Collections.
Opinions expressed by DZone contributors are their own.

Comments