How to Improve RAG Quality by Storing Knowledge Graphs in Vector Databases

Thanks to Cheney Zhang (Zilliz)

Retrieval-Augmented Generation (RAG) techniques, by integrating external knowledge bases, provide additional contextual information for LLMs, effectively alleviating issues such as hallucination and insufficient domain knowledge of LLM. However, relying solely on general knowledge bases has its limitations, especially when dealing with complex entity relationships and multi-hop questions, where the model often struggles to provide accurate answers. 

Introducing Knowledge Graphs (KGs) into the RAG system provides a new solution to this problem. KGs present entities and their relationships in a structured manner, offering more refined contextual information during retrieval. By leveraging the abundant relational data of KGs, RAG can not only pinpoint relevant knowledge more accurately but also better handle complex question-answering scenarios, such as comparing entity relationships or answering multi-hop questions.

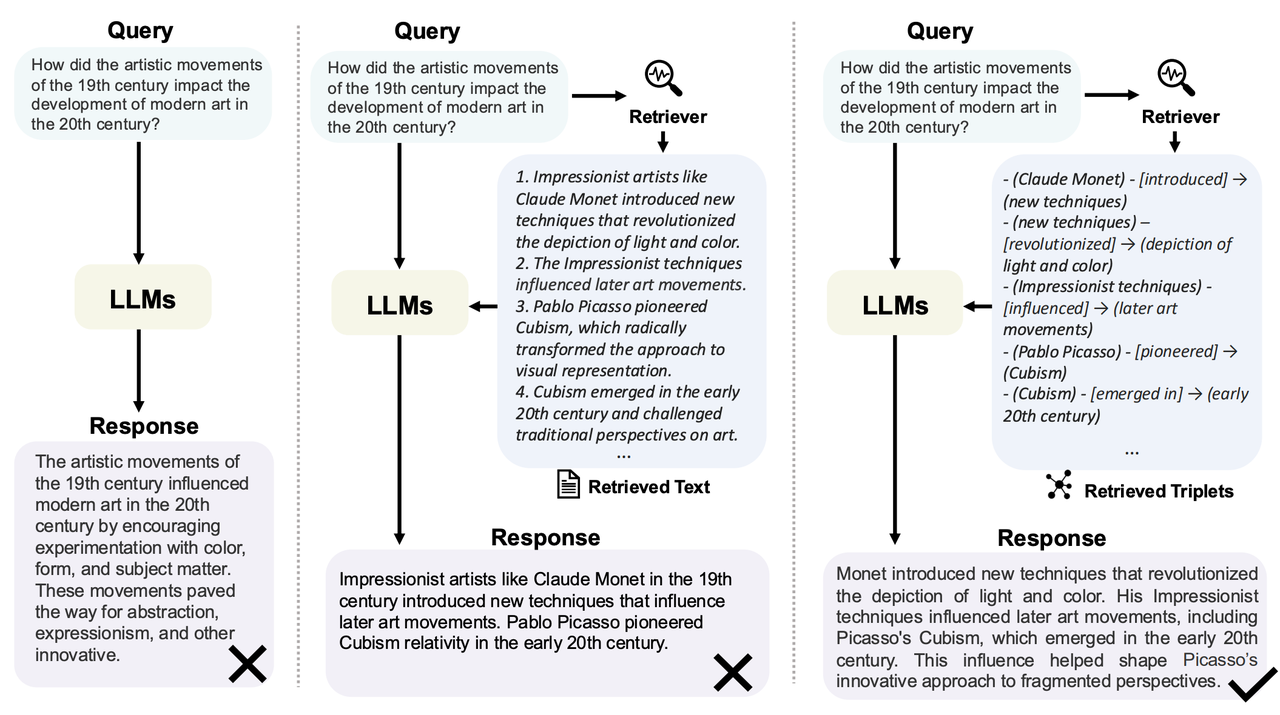
However, the current KG-RAG is still in its early exploration stage, and the industry has not yet reached a consensus on the relevant technical path; for instance, how to effectively retrieve relevant entities and relationships in the knowledge graph, how to combine vector similarity search with graph structure, there is currently no unified paradigm. 

For example, Microsoft's From Local to Global aggregates subgraph structures into community summaries through a large number of LLM requests, but this process consumes a substantial number of LLM tokens, making this approach expensive and impractical. HippoRAG uses Personalized PageRank to update the weights of graph nodes and identify important entities, but this entity-centered method is easily affected by Named Entity and Relation (NER) omissions during extraction, overlooking other information in the context. IRCoT uses multi-step LLM requests to gradually infer the final answer, but this method introduces LLM into the multi-hop search process, resulting in an extended time to answer questions, making it difficult to implement in practice.

We found that a simple RAG paradigm with multi-way retrieval and then reranking can handle complex multi-hop KG-RAG scenarios very well, without requiring excessive LLM overhead or any graph structure storage or algorithm. Despite using a very simple architecture, our method significantly outperforms current state-of-the-art solutions, such as HippoRAG, and only requires vector storage and a small amount of LLM overhead. We first introduce the theoretical basis of our method, and then describe the specific process.

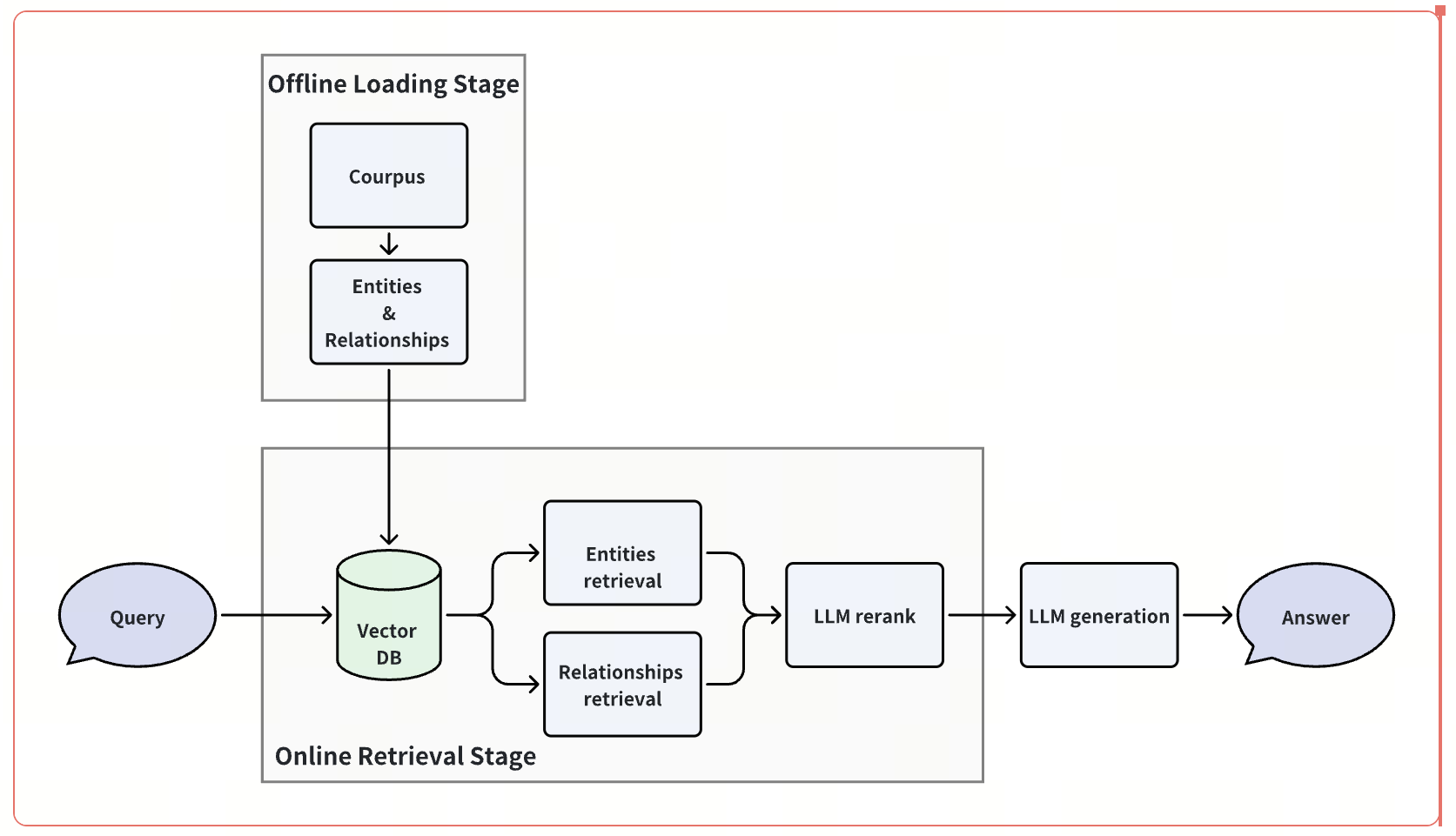
Our simple pipeline is not much different from the common multi-way retrieval and rerank architecture, but it can achieve the SoTA performance in the multihop graph RAG scenario.

Limited Hop Count Theory

In real-life KG-RAG scenarios, we noticed a concept known as limited hop count. In KG-based RAG, the actual query question only requires a limited and relatively small number of hops (usually less than four) within the knowledge graph, rather than a greater amount. Our limited hop count theory is based on two critical observations:

1. Limited complexity of queries  
2. Local dense structure of "shortcuts"

1. Limited Complexity of Queries

A user's query is unlikely to involve numerous entities or introduce complex relationships. If it does, the question would seem peculiar and unrealistic.

• Normal query: "In which year did Einstein win the Nobel Prize?"
  • Query path in the knowledge graph:
    • Find the "Einstein" node.
    • Jump to the "Nobel Prize" node associated with "Einstein".
    • Return the year the prize was awarded.
  • Hop count: 2 hops
  • Explanation: This is a standard user query, where the user wants to know a single fact directly associated with a specific entity. In this case, the knowledge graph only needs a few hops to complete the task, as all relevant information is directly linked to the central node, Einstein. This type of query is very common in practice, such as querying celebrity background information, award history, event time, etc.
• Weird query: "What is the relationship between the year the discoverer of the theory of relativity received the Nobel Prize and the number of patents they invented in a country famous for its bank secrecy laws and the magnificent scenery of the Alps?"
  • Query path in the knowledge graph:
    • Find that the "inventor" of "relativity" is "Einstein".
    • Jump to the "Nobel Prize" node associated with "Einstein".
    • Look up the year the "Nobel Prize" was awarded.
    • Identify "Switzerland" through "bank secrecy laws and the Alps".
    • Jump to the "patent" node associated with "Einstein".
    • Look up patent information related to the period in Switzerland.
    • Compare the relationship between the number of patents and the year of the award.
  • Hop count: 7 hops
  • Explanation: This question is complex, requiring not just a single fact query, but also intricate associations between multiple nodes. This type of question is not common in actual scenarios because users generally do not seek such complex cross-information in a single query. Usually, these types of questions are divided into multiple simple queries to gradually obtain information. You may think something about the number of hops sounds familiar, it's because all commonly used information is usually linkable in only a limited number of steps. You can see this in practice in the Six Degrees of Kevin Bacon.

2. Local Dense Structure of “Shortcuts”

• Alex is the child of Brian (Alex - child_of - Brian)
• Cole is married to Brian (Cole - married_to - Brian)
• Daniel is the brother of Cole (Daniel - brother_of - Cole)
• Daniel is the uncle of Alex (Daniel - uncle_of - Alex)

This is a dense knowledge graph with redundant information. The last relationship can obviously be derived from the first three relationships. However, there are often some redundant information shortcuts in the knowledge graph. These shortcuts can reduce the number of hops between some entities.

Based on these two observations, we find that the routing lookup process within the knowledge graph for a limited number of times only involves local knowledge graph information. Therefore, the process of retrieving information within the knowledge graph for a query can be implemented in the following two steps:

1. The starting point of the route can be found through vector similarity lookup. It can involve the similarity relationship lookup between the query and entities or the query and relationships.
2. The routing process to find other information from the starting point can be replaced with an LLM. Put this alternative information into the prompt, and rely on the powerful self-attention mechanism of LLM to select valuable routes. As the length of the prompt is limited, only local knowledge graph information can be put in, such as the knowledge graph information within a limited number of hops around the starting point, which is guaranteed by the limited hop count theory.

The whole process does not need any other KG storage and complex KG query statements; it only needs to use a Milvus vector database and one access of an LLM. The vector retrieval with LLM reranking is the most critical part of this pipeline, explaining why we can reach performance far beyond the methods based on graph theory (such as HippoRAG) with a traditional two-way retrieval architecture. This also shows that we do not actually need physical storage of graph structure and complex graph query SQL statements. We only need to store the logical relationship of graph structure in the vector database, a traditional architecture can perform logical sub-graph routing, and the powerful ability of modern LLM helps to achieve this.

Method Overview

Our approach solely focuses on the passage retrieval phase within the RAG process, without any novel enhancements or optimizations in chunking or LLM response generation. We assume that we have acquired a set of triplet data from the corpus, incorporating a variety of entity and relationship information. This data can symbolize the information of a knowledge graph. We vectorize the entity and relationship information individually and store them in vector storage, thus creating a logical knowledge graph. When receiving a query, the relevant entities and relationships are retrieved initially. Leveraging these entities and relationships, we perform a limited expansion on the graph structure. These relationships are integrated into the prompt along with the query question, and the LLM's capability is exploited to rerank these relationships. Ultimately, we obtain the top-K vital relationships and get the related passages within their metadata information, serving as the final retrieved passages.

Detailed Method

Vector Storage

We establish two vector storage collections: one being the entity collection, the other the relationship collection. Unique entities and relationship information are embedded into vectors via the embedding model and stored in vector storage. Entity information is directly converted into embeddings based on their word descriptions. As for the original data form of relationships, it is structured as a triplet: (Subject, Predicate, Object). We directly combine them into a sentence, which is a heuristic method: "Subject Predicate Object". For instance:

(Alex, child of, Brian) -> "Alex child of Brian"(Cole, married to, Brian) -> "Cole married to Brian"

This sentence is then directly transformed into an embedding and stored in the vector database. This approach is straightforward and efficient. Although minor grammatical issues may arise, they do not impact the conveyance of the sentence meaning and its distribution in the vector space. Of course, we also advocate for the use of LLM to generate succinct sentence descriptions during the initial extraction of triplets.

Vector Similarity Search

• For the input query, we adhere to the common paradigms in GraphRAG (such as HippoRAG and Microsoft GraphRAG), extract entities from the query, transform each query entity into an embedding, and conduct a vector similarity search on each entity collection. Subsequently, we merge the results obtained from all query entities' searches.
• For the vector search of relationships, we directly transform the query string into an embedding and perform a vector similarity search on the relationship collection.

Expanding Subgraph

We take the discovered entities and relationships as starting points in the knowledge graph and expand a certain degree outward. For the initial entities, we expand a certain number of hops outward and include their adjacent relationships, denoted as $$Set(rel1)$$. For the initial relationships, we expand a certain number of hops to obtain $$Set(rel2)$$. We then unite these two sets, $$Set(merged)=Set(rel1) \cup Set(rel2) $$.

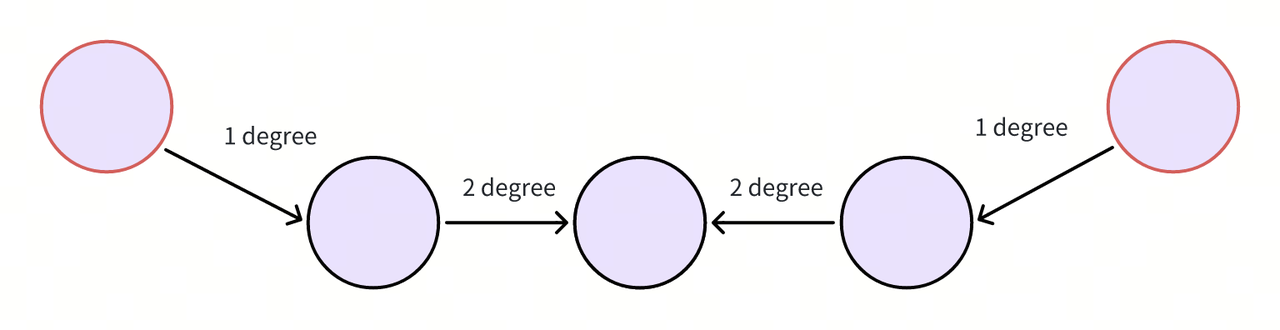
Given the limited hop count theory, we only need to expand a smaller number of degrees (like 1, 2, etc.) to encompass most of the relationships that could potentially assist in answering. Please note: the concept of the expansion degree in this step differs from the concept of the total hops required to answer a question. For instance, if answering a query involves two entities that are n hops apart, typically only an expansion of ⌈n / 2⌉ degree is necessary, as these two entities are the two starting endpoints recalled by the vector similarity. As illustrated in the figure below, the vector retrieval stage returns two red entities, and starting from them, expanding 2 degrees in opposite directions can cover a 4-hop distance, which is sufficient to answer a 4-hop question involving these two entities.

Large Language Model (LLM) Reranker

In this stage, we deploy the powerful self-attention mechanism of LLM to further filter and refine the candidate set of relationships. We employ a one-shot prompt, incorporating the query and the candidate set of relationships into the prompt, and instruct LLM to select potential relationships that could assist in answering the query. Given that some queries may be complex, we adopt the Chain-of-Thought approach, allowing LLM to articulate its thought process in its response. We have noted that this strategy provides some assistance to weaker models. We stipulate that LLM's response is in JSON format for convenient parsing.

The specific prompt is as follows:

• One shot input prompt:

I will provide you with a list of relationship descriptions. Your task is to select 3 relationships that may be useful to answer the given question. Please return a JSON object containing your thought process and a list of the selected relationships in order of their relevance.

**Question:**
When was the mother of the leader of the Third Crusade born?

**Relationship descriptions:**
[1] Eleanor was born in 1122.
[2] Eleanor married King Louis VII of France.
[3] Eleanor was the Duchess of Aquitaine.
[4] Eleanor participated in the Second Crusade.
[5] Eleanor had eight children.
[6] Eleanor was married to Henry II of England.
[7] Eleanor was the mother of Richard the Lionheart.
[8] Richard the Lionheart was the King of England.
[9] Henry II was the father of Richard the Lionheart.
[10] Henry II was the King of England.
[11] Richard the Lionheart led the Third Crusade.

• One shot output prompt:

{
  "thought_process": "To answer the question about the birth of the mother of the leader of the Third Crusade, I first need to identify who led the Third Crusade and then determine who his mother was. After identifying his mother, I can look for the relationship that mentions her birth.",
  "useful_relationships": [
    "[11] Richard the Lionheart led the Third Crusade",
    "[7] Eleanor was the mother of Richard the Lionheart",
    "[1] Eleanor was born in 1122"
  ]
}

This prompt serves as an illustrative reference. In reality, transforming the triplets in relationships into a coherent sentence can be a challenging task. However, you can certainly employ the heuristic method mentioned above to directly assemble the triplets. For instance: (Eleanor, born in, 1122) can be directly transformed into Eleanor was born in 1122. While this method may occasionally lead to certain grammatical issues, it is the quickest and most straightforward approach, and it will not mislead LLM.

Retrieving the Final Passages

For the aforementioned example, it is feasible to directly return the final response during the LLM Rerank phase; for instance, by adding a field such as "final answer" in the JSON field of the one-shot output prompt. However, the information in this prompt is exclusive to the relationship, and not all queries can yield a final answer at this juncture; hence, other specific details should be obtained from the original passage. LLM returns precisely sorted relationships. All we need to do is extract the corresponding relationship data previously stored, and retrieve the relevant metadata from it, where corresponding passage ids reside. This passage data represents the final passages that have been retrieved. The subsequent process of generating responses is identical to naive RAG, which involves incorporating them into the context of the prompt and using LLM to generate the final answer.

Results

We employ the dense embedding that aligns with HippoRAG, facebook/contriever, as our embedding model. The results show that our approach significantly surpasses both naive RAG and HippoRAG on three multi-hop datasets. All methods apply the same embedding model setting. We use Recall@2 as our evaluation metric, defined as Recall = Total number of documents retrieved that are relevant/Total number of relevant documents in the database.

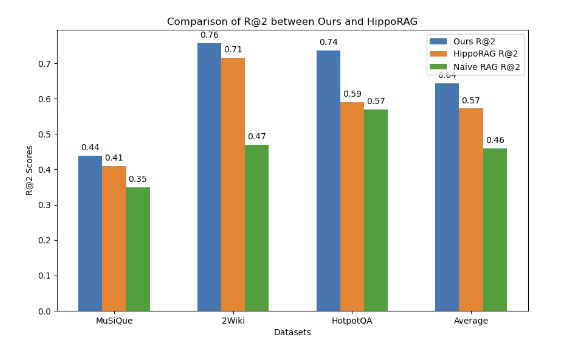
On the multi-hop datasets, our method outperforms naive RAG and HippoRAG in all datasets. All of them are compared using the same facebook/contriever embedding model.

These results suggest that even the simplest multi-way retrieval and reranking RAG paradigm, when utilized in the graph RAG context, can deliver state-of-the-art performance. It further implies that appropriate vector retrieval and LLM adoption are crucial in the multi-hop QA scenario. Reflecting on our approach, the process of transforming entities and relationships into vectors and then retrieving is like discovering the starting point of a subgraph, akin to uncovering "clues" at a crime scene. The subsequent subgraph expansion and LLM reranking resemble the process of analyzing these "clues". The LLM has a "bird's-eye view" and can intelligently select beneficial and crucial relationships from a multitude of candidate relationships. These two stages fundamentally correspond to the naive vector retrieval + LLM reranking paradigm. 

In practice, we recommend using open source Milvus, or its fully managed version Zilliz Cloud, to store and search for a large volume of entities and relationships in graph structures. For LLM, you can opt for open source models like Llama-3.1-70B or the proprietary GPT-4o mini, as mid-to-large scale models are well-equipped to handle these tasks.

For The Full Code

• Graph RAG with Milvus