Geo-Zoning Through Driving Distance Using K-Medoids Algorithm

Geo-Zoning is a method used to partition a geographical area into distinct zones or regions, with a set of rules or guidelines governing activities and land use within its boundaries using driving distance or driving time. This concept is widely used in urban planning, land use management, representatives to locate customers seamlessly, and various other fields.

The K-Medoid algorithm is a partition technique of clustering that clusters into K groups around medoids, which are data points representative of clusters; unlike the k-means algorithm, which calculates the mean for each cluster to minimize the variance, the k-Medoids algorithm selects actual data points to represent the clusters in small equidistant K groups.

Potential of leveraging the k-Medoids algorithm with a driving distance metric in advancing zoning practices. The insights garnered could pave the way for more dynamic, realistic, and efficient zoning solutions, contributing significantly to the broader discourse on urban planning and spatial analysis.

Methodology

Data Collection

• Collect the required data that needs to be partitioned into smaller K groups and cleanse or transform the data with required columns such as address, city, state, and zip code.
• Get the driving distance and latitude-longitude values for all the customers using Google or ArcGIS third-party API services and process the same in tables or flat files to create the zones using driving distance.
  • ArcGIS
  • Google

The below function helps to compute the distance matrix where each element (i, j) represents the driving distance between points i and j.

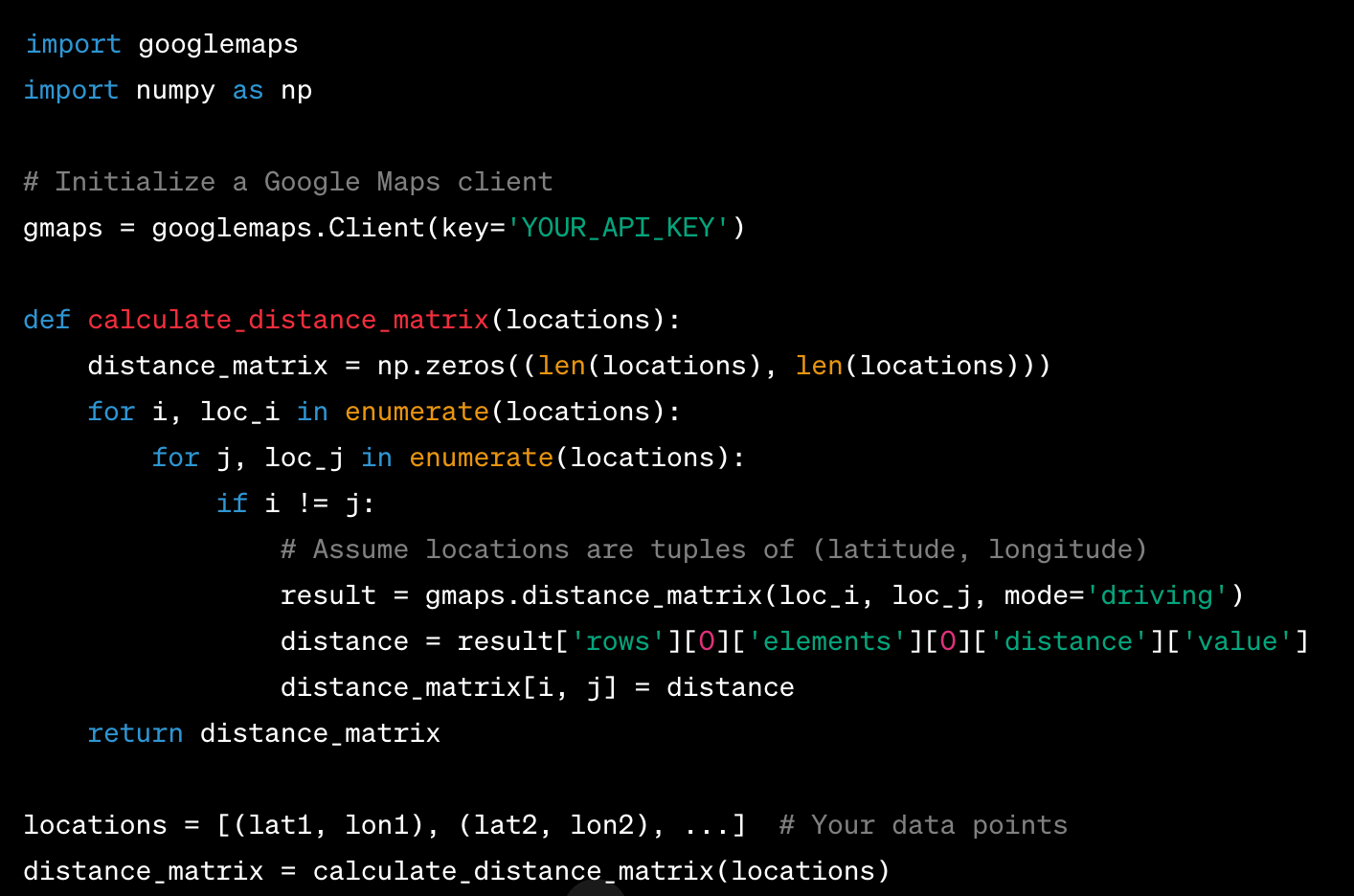
Implementation

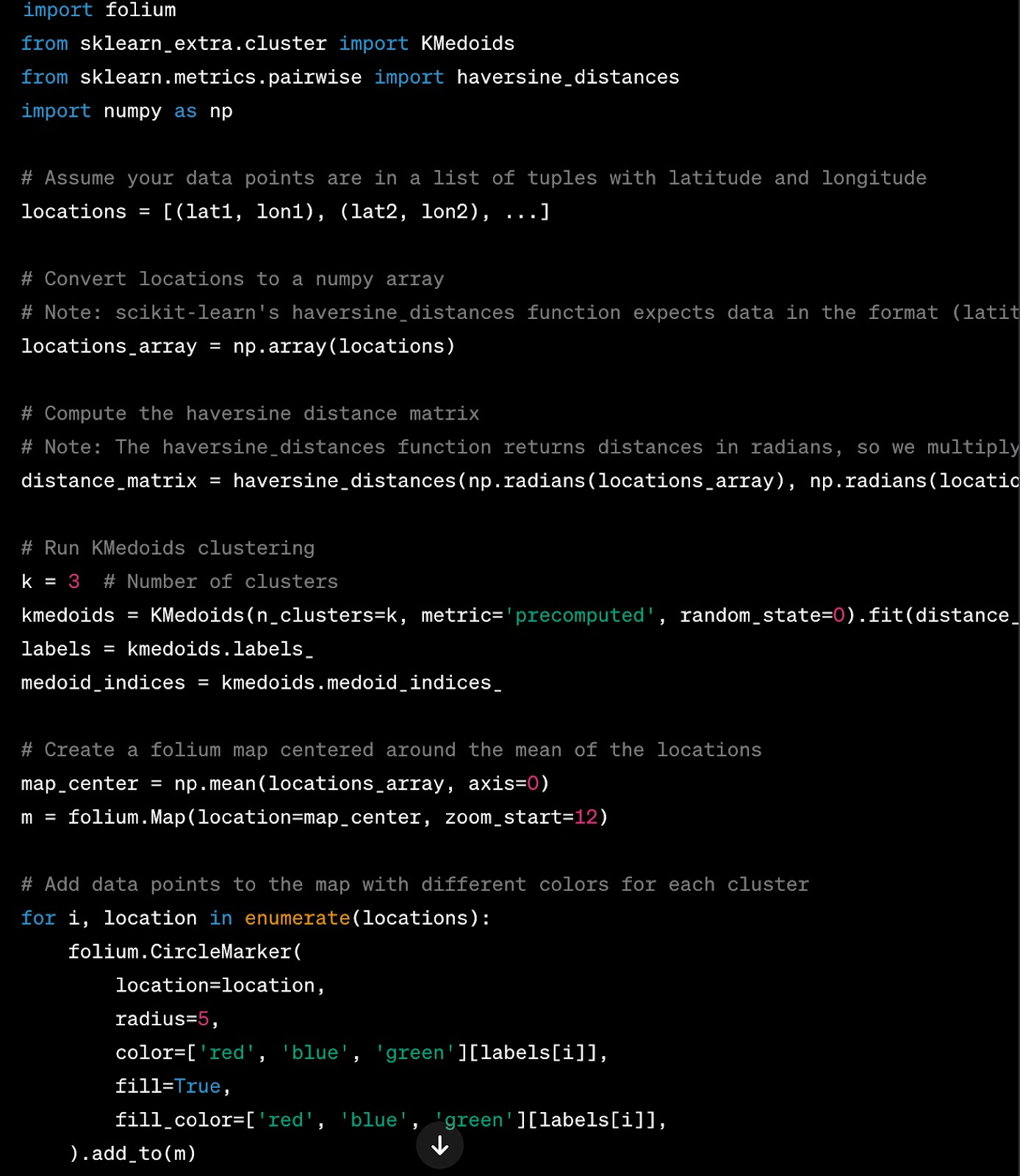
Implement the K-Medoids algorithm using scikit-learn or pyclustering libraries with the distance matrix data. Below sample code helps to create clusters using distance matrix data captured in the previous step.

• We first calculate the haversine distance matrix. The haversine formula calculates the shortest distance between two points on the surface of a sphere using their latitudes and longitudes measured along the surface.
• We then run the KMedoids clustering algorithm using the KMedoids class from scikit-learn-extra, passing the precomputed distance matrix to it.
• Finally, we use folium to create a map visualization of the clusters. Each data point is shown as a small circle with different colors for different clusters, and the medoids are shown as larger black circles.

Experimentation

Optimal numbers of zones or clusters can be determined using the Elbow Method or Silhouette Score to ensure the effectiveness of the k-medoid algorithm.

Elbow Method

• The Elbow Method is a common technique for finding an optimal K value. By plotting the explained variation as a function of the number of clusters and selecting the "elbow" of the curve as the number of clusters to use.
• In the context of K-Medoids, you could plot the sum of distances to the medoids as a function of the number of clusters.

Silhouette Score

• The silhouette score is a measure of how similar an object is to its own cluster (cohesion) compared to other clusters (separation).
• The silhouette score ranges from -1 to 1. If the score is near 1, the cluster assignments are appropriate. If the score is near -1, the cluster assignments are incorrect.

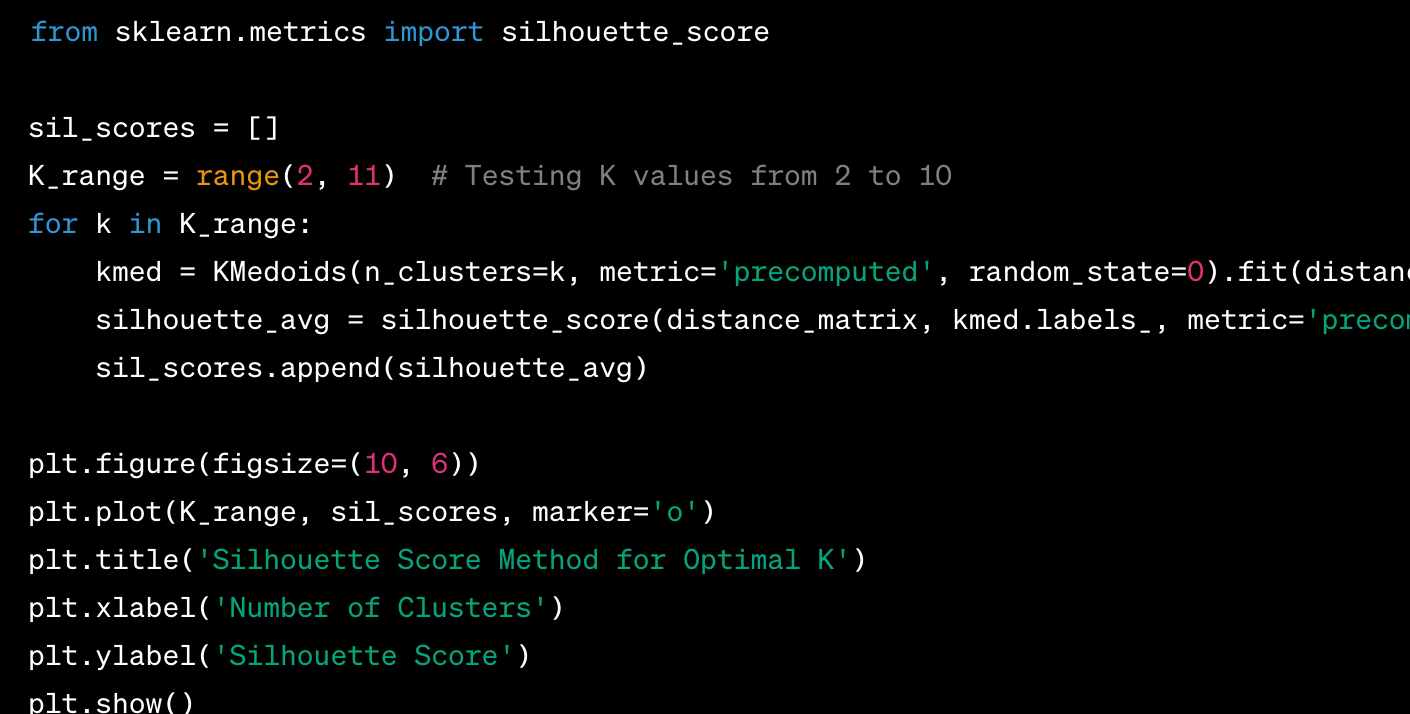
These methods can help in tuning the K-Medoids algorithm to achieve better clustering results based on the specific data and problem at hand.

Conclusion

Implementing the K-Medoids algorithm with driving distance can be computationally intensive, especially if online APIs are used to calculate driving distances on-the-fly. It's often more efficient if a precomputed distance matrix is available in our database or flat file. Geo-zoning helps various industries to enhance the effectiveness and efficiency of work at a faster pace in a well planned manner, which in turn improves productivity of individuals and companies.

Frequently Asked Questions

Data Requirements to Implement Zoning?

Identify the targeted customer list with address and geographic information, extract driving distance between one to many customers through ArcGIS or Google API’s and apply algorithms to generate zoning.

Optimal Number of Clusters Determined in the K-Medoids Algorithm? 

Apply Elbow method and silhouette analysis to determine the number of zones based required parameters, which suits domain specific and application specific requirements.