Deadlock-Free Synchronization in Java

Thread synchronization is a great tool to overcome race conditions in multithreaded programs. But, it also has a dark side; deadlocks: nasty errors that are difficult to discover, reproduce, and fix. The only surefire way to prevent them is properly designing your code, which is the subject of this article. We will take a look at the origin of deadlocks, consider a method for discovering potential deadlocks in existing code, and present practical approaches to designing a deadlock-free synchronization. The concepts will be illustrated with a simple demo project.

It is assumed that the reader is already familiar with multithreaded programming and has a good understanding of thread synchronization primitives in Java. In the following sections, we will not distinguish between the synchronized statements and the lock API, using the term “lock” for reentrant locks of both types, preferring the former in the examples.

1. Mechanism of Deadlocks

Let’s recap on how the deadlocks work. Consider the following two methods:

xxxxxxxxxx

void increment(){

  synchronized(lock1){

    synchronized(lock2){

      variable++;

    }

  }

}

void decrement(){

  synchronized(lock2){

    synchronized(lock1){

      variable--;

    }

  }

}

The methods are intentionally designed to produce deadlocks. Let’s consider in detail how this happens.

Both increment() and decrement() basically consist of the following 5 steps:

Table 1

Obviously, steps 1 and 2 in both methods are passable only if the corresponding locks are free, otherwise, the executing thread would have to wait for their release.

Suppose there are two parallel threads, one executing the increment() and another executing the decrement(). Each thread’s steps will be performed in the normal order, but, if we consider both threads together, the steps of one thread will be randomly interleaved with the steps of another thread. The randomness comes from unpredictable delays imposed by the system thread scheduler. The possible interleaving patterns, or scenarios, are quite numerous (to be exact, there are 252 of them) and may be divided into two groups. The first group is where one of the threads is quick enough to acquire both locks (see Table 2).

Table 2

All the cases in this group result in a successful completion.

In the second group, both threads succeed in acquiring a lock. The outcome can be seen in Table 3:

Table 3

All the cases in this group result in the situation where the first thread waits for the lock that is owned by the second thread, and the second thread waits for the lock that is owned by the first thread, so both threads cannot progress any further: 

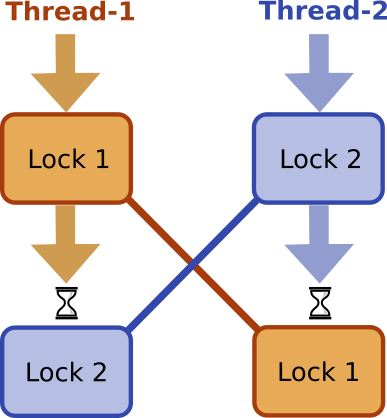
Figure 1

This is a classic deadlock situation with all its typical properties. Let’s outline the important ones:

• There are at least two threads, each taking at least two locks.
• A deadlock happens only at a certain combination of thread timings.
• The occurrence of a deadlock depends on the locking order.

The second property means that deadlocks cannot be reproduced at will. Moreover, their reproducibility depends on the OS, CPU frequency, CPU load, and other factors. The latter means that the concept of software testing just doesn’t work for deadlocks, because the same code may work flawlessly on one system and fail on another. So, the only way to deliver a correct application is to eliminate deadlocks by the very design. There exist two basic approaches to such design, and, now, let’s start with the simpler one.

2. Coarse-Grained Synchronization

From the first property in the above list, it follows that if no thread in our application is allowed to hold more than one lock at once, deadlocks will not happen. Ok, this sounds like a plan, but how many locks should we use and where to place them?

The simplest and most straightforward answer is to protect all the transactions with a single lock. For example, to protect a complex data object, you may just declare all its public methods as synchronized. This approach is used in java.util.Hashtable. The price for simplicity is the performance penalty due to the lack of concurrency, as all the methods are mutually blocking.

Fortunately, in many cases the coarse-grained synchronization may be performed in a less restrictive way, allowing for some concurrency and better performance. To explain it, we should introduce a concept of transactionally connected variables. Let’s say that two variables are transactionally connected if any of the two conditions is met:

1. There exists a transaction that involves both variables.
2. Both variables are connected to a third variable (transitivity).

So, you start with grouping variables in such a way that any two variables in the same group are transactionally connected while any two variables in different groups aren’t. Then you protect each group by a separate dedicated lock:

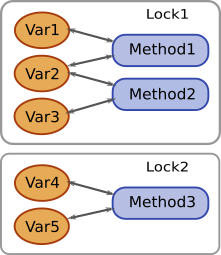
Figure 2

The above explanation is somewhat short on the exact meaning of the terms “transaction” and “involves”, but doing it accurately would be too long for this article, if at all possible, so it’s left on the reader’s intuition and experience.

 A good real-life example of such advanced coarse-grained synchronization is java.util.concurrent.ConcurrentHashMap. Inside this object, there is a number of identical data structures (“buckets”), and each bucket is protected by its own lock. A transaction is dispatched to a bucket that is determined by the key’s hashcode. As a result, transactions with different keys mostly go to different buckets, which allows them to be executed concurrently without sacrificing thread safety, which is possible due to the transactional independence of the buckets.

However, some solutions require a much higher level of concurrency than may be achieved with coarse-grained synchronization. Later, we will consider how to approach this, but first, we need to introduce an efficient method for the analysis of synchronization schemes.

3. Locking Diagrams

Suppose you need to decide if a given code contains a potential deadlock. Let’s call such kind of task a “synchronization analysis” or “deadlock analysis”. How would you approach this? 

Most likely, you would try to sort in mind through all the possible scenarios of threads’ contention over the locks, trying to figure out if a bad scenario exists. In Section 1, we took such a straightforward approach and it turned out that there are too many scenarios. Even in the simplest possible case, there are 252 ones, so exhaustively checking them all is out of practical reach. In practice, you would probably end up considering only a few scenarios and hoping you didn’t miss something important. In other words, fair deadlock analysis cannot be done with a naïve approach, we need a specialized, more efficient method.

This method consists of building a locking diagram and checking it for the presence of circular dependencies. A locking diagram is a graph that displays the locks and the threads’ interactions over these locks. Each closed loop in such a diagram indicates a possible deadlock, and the absence of closed loops guarantees deadlock-safety of the code.

Here is the recipe for drawing a locking diagram. It uses the code from Section 1 as an example:

1. For each lock in the code put a corresponding node on the diagram; in the example these are lock1 and lock2
2. For all statements where a thread tries to acquire lock B while already holding lock A, draw an arrow from node A to node B; in the example, there will be ‘lock1 -> lock2’ in the increment() and lock2 -> lock1 in the decrement(). If a thread takes several locks in a sequence, draw an arrow for each consecutive two locks.

The final diagram for the example in Section 1 looks like this:

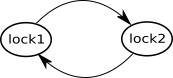
Figure 3

It has a closed-loop: lock1 -> lock2 -> lock1, which instantly tells us that the code contains a potential deadlock. Cute, isn’t it?

Let’s do one more exercise. Consider the following code:

x

void transaction1(int amount) {

  synchronized(lock1) {

    synchronized(lock2) {

      // do something

    }

  }

}

void transaction2(int amount) {

  synchronized(lock2) {

    synchronized(lock3) {

      // do something

    }

  }

} 

void transaction3(int amount) {

  synchronized(lock3) {

    synchronized(lock1) {

      // do something

    }

  }

}

Let’s find out whether this code is deadlock-safe. There are 3 locks: lock1, lock2, lock3and 3 locking paths: lock1 -> lock2 in transaction1(), lock2 -> lock3 in transaction2(), lock3 -> lock1 in transaction3().

The resulting diagram is depicted in Figure 4-A:

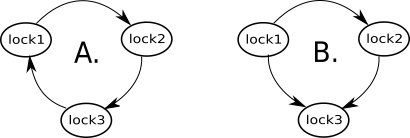
Figure 4

Again, this diagram instantly indicates that our design contains a potential deadlock. But, not only that. It also hints us how to fix the design; we just need to break the loop! For example, we can swap the locks in the method transaction3(). The corresponding arrow changes direction and the diagram in Figure 4-B become loop-free, which guarantees the deadlock-safety of the fixed code.

Now that we are familiar with the magic of diagrams, we are ready to move on to the more complicated yet more efficient approach to designing deadlock-free synchronization.

4. Fine-Grained Synchronization With Lock Ordering

This time, we take the route of making the synchronization as fine-grained as possible, in the hope to get in return the maximum possible concurrency of transactions. This design is based on two principles.

The first principle is to forbid any variable from participating in more than one transaction at once. To implement this we associate each variable with a unique lock and start each transaction by acquiring all the locks associated with the involved variables. The following code illustrates this:

x

void transaction(Item i1, Item i2, Item i3, double amount) {

  synchronized(i1.lock) {

    synchronized(i2.lock) {

      synchronized(i3.lock) {

        // do actual transaction on the items

      }

    }

  }

}

Once the locks are acquired, no other transaction can access the variables, so they are safe from concurrent modification. This means that all transactions in the system are consistent. At the same time, transactions over non-intersecting sets of variables are allowed to run concurrently. Thus, we obtain a highly concurrent yet thread-safe system.

But, such a design immediately incurs a possibility of deadlocks because now we deal with multiple threads and multiple locks per thread.

Then, the second design principle comes into play, which states that locks must be acquired in a canonical order to prevent deadlocks. This means that we associate each lock with a unique constant index, and always acquire locks in the order defined by their indices. Applying this principle to the code above we obtain the complete illustration of the fine-grained design:

x

void transaction(Item i1, Item i2, Item i3, double… amounts) {

  // Our plan is to use item IDs as canonical indices for locks

  Item[] order = {i1, i2, i3};

  Arrays.sort(order, (a,b) -> Long.compare(a.id, b.id));

  synchronized(order [0].lock) {

    synchronized(order[1].lock) {

      synchronized(order[2].lock) {

        // do actual transaction on the items

      }

    }

  }

}

But, is it for sure that canonical ordering does prevent deadlocks? Can we prove it? The answer is yes, we can do it using locking diagrams.

Suppose we have a system with N variables, so there are N-associated locks and therefore N nodes on the diagram. Without forced ordering the locks would be grabbed in a random order, so on the diagram, there would be random arrows going in both directions, and, for sure, there would exist closed loops indicating deadlocks:

Figure 5

If we enforce lock ordering, the locking paths from higher to lower index will be excluded, so the only remaining arrows will be those going from the left to the right:

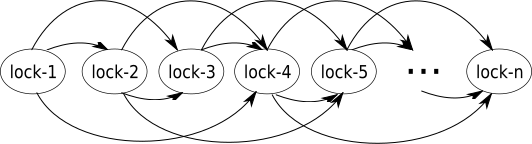
Figure 6

We won’t find a closed-loop on this diagram no matter how hard we try because closed loops may exist only if there are arrows going in both directions, which is not the case. And, no closed loops means no deadlocks. The proof is complete.

Well, by using fine-grained locking along with lock ordering we can build a system that is highly concurrent, thread-safe, and deadlock-free. But, is there a price to pay for improved concurrency? Let’s consider.

First, in a low-concurrency situation, there is some speed loss compared to the coarse-grained method. Each lock capture is a rather expensive operation, yet the fine-grained design assumes at least twice as many locks captures. But, as the number of concurrent requests grows, the fine-grained design quickly becomes superior thanks to the use of multiple CPU cores.

Second, there is a memory overhead due to a large number of lock objects. Fortunately, this is easy to fix. If the protected variables are objects, we can get rid of the separate lock objects whatsoever and use the variables themselves as their own locks. Otherwise, e.g. if the variables are primitive array elements, we may get by with only a limited number of extra objects. To this end, we define a mapping from a variable ID into a moderately-sized array of locks. In such a case the locks must be sorted by their actual indices, not by the variable IDs.

And last, but not least, is the code complexity. While the coarse-grained design may be accomplished just by declaring some methods synchronized, the fine-grained approach requires a fair amount of a rather hairy code to be written, sometimes we may even need to mess with the business logic. Such code requires careful writing and is more difficult to maintain. Unfortunately, this difficulty cannot be worked around, but the result is worth the hassle, which will be demonstrated below.

5. Demo Project

To see how the proposed design patterns look in a real code, let’s look at the simple demo project. The project goal is to build a library that mocks some of the basic functionality of a bank. For brevity it uses a fixed set of accounts and implements only the four operations: querying the balance, depositing, withdrawing, and transferring funds between accounts.  To make the task more interesting, it is required that the account balances may not be negative nor may exceed a certain value. The transactions resulting in a violation of these rules should be rejected. The library API is defined in the interface MockBank.

There are three implementations of this interface using different synchronization approaches described above:

• CoarseGrainedImpl uses coarse-grained synchronization.
• FineGrainedImpl uses a basic version of the fine-grained synchronization.
• FineGrainedWithMappingImpl uses a memory-efficient version of the fine-grained synchronization.

There is also a test for the performance and correctness of the implementations, the MockBankCrashTest. Each source file contains a detailed description of the algorithm in the class comment. Multiple test runs showed neither thread safety violations nor deadlocks. On a multicore system, the performance of the fine-grained designs was several times that of the coarse-grained one, right as expected.

All project files are here.

6. Hidden Locks

Up to this point, it could seem that the proposed design patterns automatically solve any synchronization problem. While this is not completely untrue, there exist gotchas you should be aware of.

The considerations in the above sections, though correct and valid in themselves, don’t take into account the environment. Generally, this is a mistake, since our code inevitably has to interact with the OS and libraries, where there may exist hidden locks which may interfere with our synchronization code, causing unexpected deadlocks. Let’s see an example. Consider the following code:

x

private Hashtable<String, Long> db = new Hashtable<>();

private long version;

public void put(String key, long value){

  updateVersion(key);

  db.put(key, value);

}

public long increment(String key){

  db.computeIfPresent(key, (k,v)->{

    updateVersion(k);

    return v+1;

  });

}

private synchronized void updateVersion(String key){

  db.put(key+".version", version++);

}

At the first glance, this code should be deadlock-free because there is only a single lock in the updateVersion(). But, this impression is wrong because there actually exists an extra hidden lock in the Hashtable instance. The call chains put()-updateVersion() and increment()-computeIfPresent()-updateVersion() take these two locks in the opposite order, which results in potential deadlocks.

An experienced reader might rightly argue here that the code above is rather lame and deliberately crafted to cause deadlocks. Then, here comes the cleaner example, where we attempt to swap atomically two values in the mapping:

x

private final Map<Integer, String> map = new ConcurrentHashMap<>();

{

  map.put(1, "1");

  map.put(2, "2");

}

public void swapValues(Integer key1, Integer key2) {

  map.compute(key1, (k1, v1) -> {

    return map.put(key2, v1); // returns v2

  });

}

This time, there are no locks at all, and the code looks perfectly legit but, nevertheless, we again meet potential deadlocks. The cause is the internal design of the ConcurrentHashMap, which was outlined in Section 2. The calls to swapValues(1,2) and swapValues(2,1) acquire the corresponding buckets’ locks in the opposite order, which means the code is potentially deadlocking. This is why the documentation  ConcurrentHashMap.compute() strongly discourages attempting to alter the map from within a callback. Unfortunately, in many cases, such warnings are missing from the documentation.

As the above examples show, the interference with hidden locks is most likely to happen in the callback methods. So it is recommended to keep the callbacks short, simple, and free of calls to synchronized methods. If this is not possible, you should always keep in mind that the thread executing the callback may be holding one or more hidden locks, and plan the synchronization accordingly.

Conclusion

In this article, we explored the problem of deadlocks in multithreaded programming. We found that deadlocks can be completely avoided if synchronization code is written according to certain design patterns. We also studied why and how such designs work, what the limits of their applicability are, and how to efficiently find and fix the potential deadlocks in the existing code. It is expected that the material presented provides a sufficient practical guide to the design of perfect deadlock-free synchronization.

All source files may be downloaded from Github as a zip archive.