A Comprehensive Guide to Random Forest in R
This article provides an explanation of the random forest algorithm in R, and it also looks at classification, a decision tree example, and more.
Join the DZone community and get the full member experience.
Join For Free
Random Forest in R
With the demand for more complex computations, we cannot rely on simplistic algorithms. Instead, we must utilize algorithms with higher computational capabilities and one such algorithm is the random forest. In this blog post on random forest In R, you’ll learn the fundamentals of random forest along with its implementation by using the R Language.
What Is Classification?
Classification is the method of predicting the class of a given input data point. Classification problems are common in machine learning and they fall under the Supervised learning method.
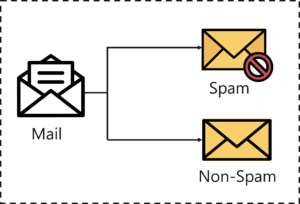
Let’s say you want to classify your emails into 2 groups: spam and non-spam emails. For this kind of problem, where you have to assign an input data point into different classes, you can make use of classification algorithms.
Under classification we have 2 types:
- Binary Classification
- Multi-Class Classification
Classification — Random Forest In R
The example that I gave earlier about classifying emails as spam and non-spam is of binary type because here we’re classifying emails into 2 classes (spam and non-spam).
But let’s say that we want to classify our emails into 3 classes:
- Spam messages
- Non-Spam messages
- Drafts
So here we’re classifying emails into more than 2 classes, this is exactly what multi-class classification means.
One more thing to note here is that it is common for classification models to predict a continuous value. But this continuous value represents the probability of a given data point belonging to each output class.
Now that you have a good understanding of what classification is, let’s take a look at a few classification algorithms used in machine learning.
What Is Random Forest?
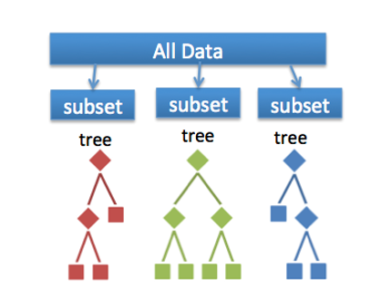
The random forest algorithm is a supervised classification and regression algorithm. As the name suggests, this algorithm randomly creates a forest with several trees.
Generally, the more trees in the forest, the more robust the forest looks like. Similarly, in the random forest classifier, the higher the number of trees in the forest, the greater is the accuracy of the results.
Random Forest
In simple words, random forest builds multiple decision trees (called the forest) and glues them together to get a more accurate and stable prediction. The forest it builds is a collection of decision trees, trained with the bagging method.
Before we discuss random forest in-depth, we need to understand how decision trees work.
Are Random Forest and Decision Trees the Same?
Let’s say that you’re looking to buy a house, but you can't decide which one to buy. So, you consult a few agents, and they give you a list of parameters that you should consider before buying a house. The list includes:
- Price of the house
- Locality
- Number of bedrooms
- Parking space
- Available facilities
These parameters are known as predictor variables, which are used to find the response variable. Here’s a diagrammatic illustration of how you can represent the above problem statement using a decision tree.
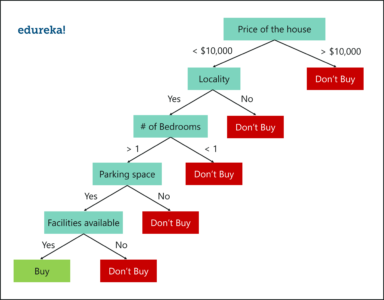
Decision Tree Example
An important point to note here is that decision trees are built on the entire dataset by making use of all the predictor variables.
Now let’s see how random forest would solve the same problem.
Like I mentioned earlier, random forest is an ensemble of decision trees, and it randomly selects a set of parameters and creates a decision tree for each set of chosen parameters.
Take a look at the below figure.
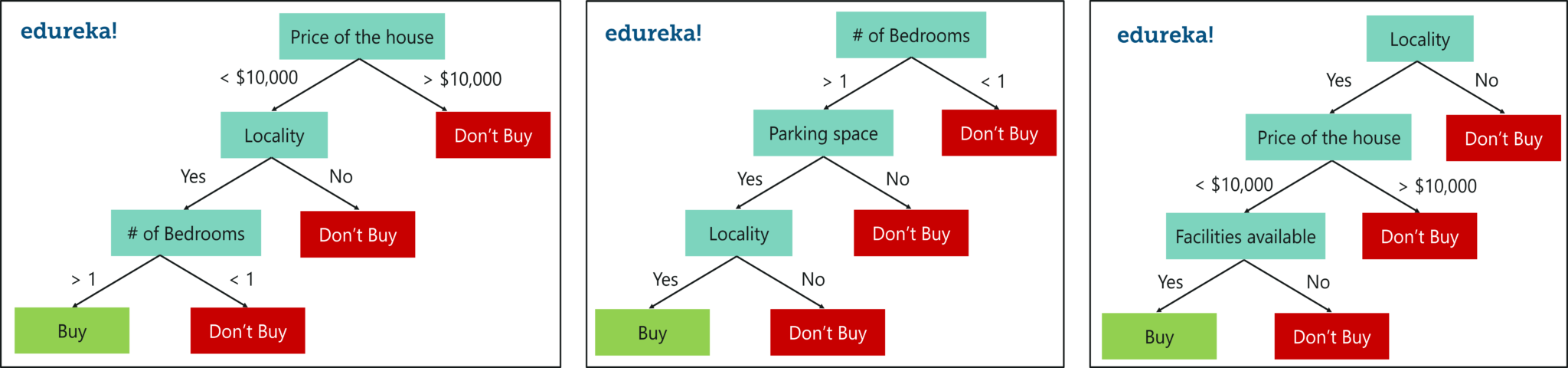
Random Forest With 3 Decision Trees
Here, I’ve created 3 decision trees, and each is taking only 3 parameters from the entire dataset. Each decision tree predicts the outcome based on the respective predictor variables used in that tree and finally takes the average of the results from all the decision trees in the random forest.
Put more simply, after creating multiple decision trees using this method, each tree selects or votes the class (in this case, the decision trees will choose whether or not a house is bought), and the class receiving the most votes by a simple majority is termed as the predicted class.
To conclude, decision trees are built on the entire dataset using all the predictor variables, whereas random forests are used to create multiple decision trees, such that each decision tree is built only on a part of the data set.
I hope the difference between decision trees and random forest is clear.
Why Use Random Forest?
Even though decision trees are convenient and easily implemented, they lack accuracy. Decision trees work very effectively with the training data that was used to build them, but they’re not flexible when it comes to classifying the new sample, which means that the accuracy during the testing phase is very low.
This happens due to a process called Over-fitting.
This means that the disturbance in the training data is recorded and learned as concepts by the model. But the problem here is that these concepts do not apply to the testing data and negatively impact the model’s ability to classify the new data, hence reducing the accuracy of the testing data.
This is where random forest comes in. It is based on the idea of bagging, which is used to reduce the variation in the predictions by combining the result of multiple decision trees on different samples of the dataset.
Now let’s focus on random forest.
How Does Random Forest Work?
To understand random forest, consider the below sample dataset. In it, we have four predictor variables:
- Weight
- Blood flow
- Blocked Arteries
- Chest Pain
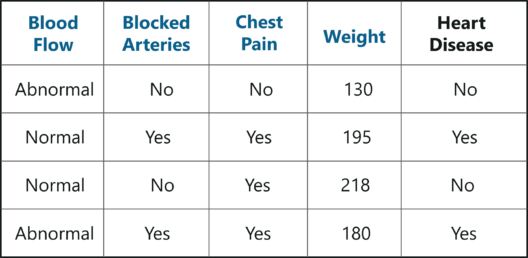
These variables are used to predict whether or not a person has heart disease. We’re going to use this dataset to create a random forest that predicts if a person has heart disease or not.
Creating A Random Forest
Step 1: Create a Bootstrapped Dataset
Bootstrapping is an estimation method used to make predictions on a dataset by re-sampling it. To create a bootstrapped dataset, we must randomly select samples from the original dataset. A point to note here is that we can select the same sample more than once.
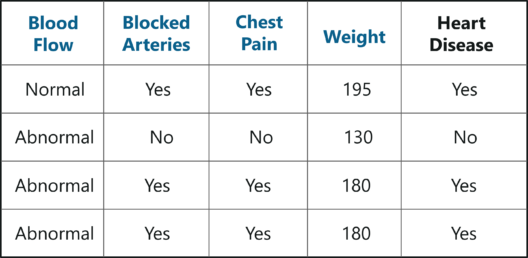
In the above figure, I have randomly selected samples from the original dataset and created a bootstrapped dataset. Simple, isn’t it? Well, in real-world problems, you’ll never get such a small dataset, thus creating a bootstrapped dataset is a little more complex.
Step 2: Creating Decision Trees
- Our next task is to build a decision tree by using the bootstrapped dataset created in the previous step. Since we’re making a random forest, we will not consider the entire dataset that we created. Instead, we’ll only use a random subset of variables at each step.
- In this example, we’re only going to consider two variables at each step. So, we begin at the root node, here we randomly select two variables as candidates for the root node.
- Let’s say we selected Blood Flow and Blocked Arteries. Out of these 2 variables, we must now select the variable that best separates the samples. For the sake of this example, let’s say that Blocked Arteries is a more significant predictor and thus assign it as the root node.
- Our next step is to repeat the same process for each of the upcoming branch nodes. Here, we again select two variables at random as candidates for the branch node and then choose a variable that best separates the samples.
Just like this, we build the tree by only considering random subsets of variables at each step. By following the above process, our tree would look something like this:
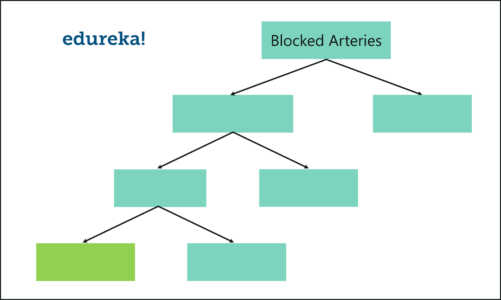
We just created our first decision tree.
Step 3: Go Back to Step 1 and Repeat
Like I mentioned earlier, random forest is a collection of decision trees. Each decision tree predicts the output class based on the respective predictor variables used in that tree. Finally, the outcome of all the decision trees in a random forest is recorded and the class with the majority votes is computed as the output class.
Thus, we must now create more decision trees by considering a subset of random predictor variables at each step. To do this, go back to step 1, create a new bootstrapped dataset, and then build a decision tree by considering only a subset of variables at each step. So, by following the above steps, our random forest would look something like this:
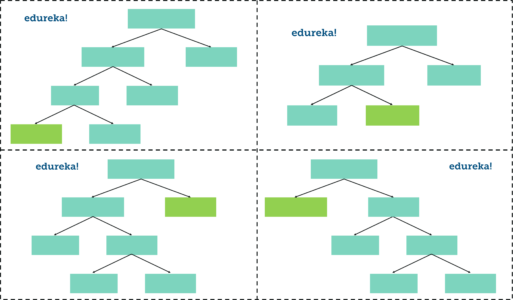
This iteration is performed 100’s of times, therefore creating multiple decision trees with each tree computing the output, by using a subset of randomly selected variables at each step.
Having such a variety of decision trees in a random forest is what makes it more effective than an individual decision tree created using all the features and the whole dataset.
Step 4: Predicting the Outcome of a new data point
Now that we’ve created a random forest, let’s see how it can be used to predict whether a new patient has heart disease or not.
The below diagram has data about the new patient. All we have to do is run this data down the decision trees that we made.
The first tree shows that the patient has heart disease, so we keep a track of that in a table as shown in the figure.
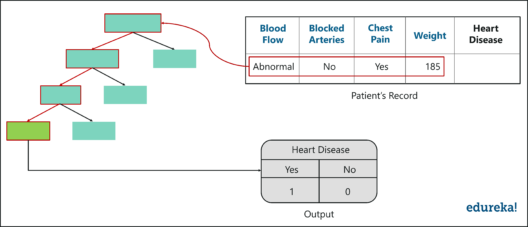
Similarly, we run this data down the other decision trees and keep a track of the class predicted by each tree. After running the data down all the trees in the random forest, we check which class got the majority votes. In our case, the class ‘Yes’ received the most number of votes, hence it’s clear that the new patient has heart disease.
To conclude, we bootstrapped the data and used the aggregate from all the trees to make a decision, this process is known as Bagging.
Step 5: Evaluate the Model
Our final step is to evaluate the random forest model. Earlier while we created the bootstrapped dataset, we left out one entry/sample since we duplicated another sample. In a real-world problem, about 1/3rd of the original dataset is not included in the bootstrapped dataset.
The below figure shows the entry that didn’t end up in the bootstrapped dataset.
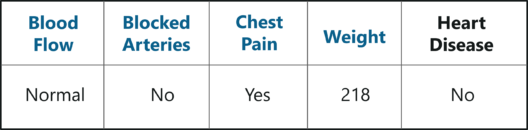
This sample dataset that does not include in the bootstrapped dataset is known as the Out-Of-Bag (OOB) dataset. The Out-Of-Bag dataset is used to check the accuracy of the model since the model wasn’t created using this OOB data it will give us a good understanding of whether the model is effective or not.
In our case, the output class for the OOB dataset is ‘No’. So, in order for our random forest model to be accurate, if we run the OOB data down the decision trees, we must get a majority of ‘No’ votes. This process is carried out for all the OOB samples, in our case we only had one OOB, however, in most problems, there are usually many more samples.
Therefore, eventually, we can measure the accuracy of a random forest by the proportion of OOB samples that are correctly classified.
The proportion of OOB samples that are incorrectly classified is called the Out-Of-Bag Error. So that was an example of how random forest works.
Now let’s get our hands dirty and implement the random forest algorithm to solve a more complex problem.
Practical Implementation of Random Forest in R
Even people living under a rock would’ve heard of a movie called Titanic. But how many of you know that the movie is based on a real event? Kaggle assembled a dataset containing data on who survived and who died on the Titanic.
Problem Statement: To build a random forest model that can study the characteristics of an individual who was on the Titanic and predict the likelihood that they would have survived.
Dataset Description: There are several variables/features in the dataset for each person:
- pclass: passenger class (1st, 2nd, or 3rd)
- sex
- age
- sibsp: number of Siblings/Spouses Aboard
- parch: number of Parents/Children Aboard
- fare: how much the passenger paid
- embarked: where they got on the boat (C = Cherbourg; Q = Queenstown; S = Southampton)
We’ll be running the below code snippets in R by using RStudio, so go ahead and open up RStudio. For this demo, you need to install the caret package and the randomForest package.
install.packages("caret", dependencies = TRUE)
install.packages("randomForest")The next step is to load the packages into the working environment.
library(caret)
library(randomForest)It’s time to load the data; we will use the read.table function to do this. Make sure you mention the path to the files (train.csv and test.csv)
train <- read.table('C:/Users/zulaikha/Desktop/titanic/train.csv', sep=",", header= TRUE)The above command reads in the file “train.csv”, using the delimiter “,”, (which shows that the file is a CSV file) including the header row as the column names, and assigns it to the R object train.
Now, let’s read in the test data:
test <- read.table('C:/Users/zulaikha/Desktop/titanic/test.csv', sep = ",", header = TRUETo compare the training and testing data, let’s take a look at the first few rows of the training set:
head(train)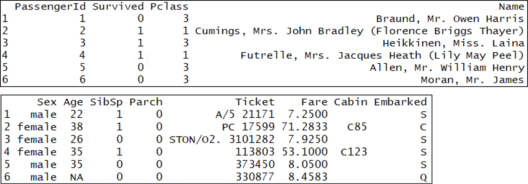
You’ll notice that each row has a column “Survived,” which is a probability between 0 and 1 if the person survived this value is above 0.5 and if they didn’t it is below 0.5. Now, let’s compare the training set to the test set:
head(test)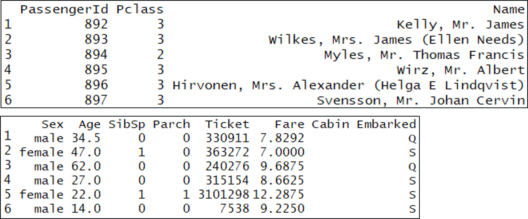 The main difference between the training set and the test set is that the training set is labeled, but the test set is unlabeled. The train set obviously doesn’t have a column called “Survived” because we have to predict that for each person who boarded the titanic.
The main difference between the training set and the test set is that the training set is labeled, but the test set is unlabeled. The train set obviously doesn’t have a column called “Survived” because we have to predict that for each person who boarded the titanic.
Before we get any further, the most essential factor while building a model is picking the best features to use in the model. It’s never about picking the best algorithm or using the most sophisticated R package. Now, a “feature” is just a variable.
So, this brings us to the question, how do we pick the most significant variables to use? The easy way is to use cross-tabs and conditional box plots.
Cross-tabs represent relations between two variables in an understandable manner. In accordance to our problem, we want to know which variables are the best predictors for “Survived”. Let’s look at the cross-tabs between “Survived” and each other variable. In R, we use the table function:
table(train[,c('Survived', 'Pclass')])
Pclass
Survived 1 2 3
0 80 97 372
1 136 87 119From the cross-tab, we can see that “Pclass” could be a useful predictor of “Survived.” This is because the first column of the cross-tab shows that, of the passengers in Class 1, 136 survived and 80 died (i.e. 63% of first-class passengers survived). On the other hand, in Class 2, 87 survived and 97 died (i.e. only 47% of second class passengers survived). Finally, in Class 3, 119 survived and 372 died (i.e. only 24% of third-class passengers survived). This means that there’s an obvious relationship between the passenger class and the survival chances.
Now we know that we must use Pclass in our model because it definitely has a strong predictive value of whether someone survived or not. Now, you can repeat this process for the other categorical variables in the dataset, and decide which variables you want to include
To make things easier, let’s use the “conditional” box plots to compare the distribution of each continuous variable, conditioned on whether the passengers survived or not. But first we’ll need to install the ‘fields’ package:
install.packages("fields")
library(fields)
bplot.xy(train$Survived, train$Age)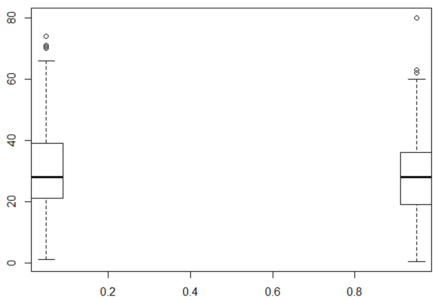 Box Plot – Random Forest In R
Box Plot – Random Forest In R
The box plot of age for people who survived and who didn’t is nearly the same. This means that the Age of a person did not have a large effect on whether one survived or not. The y-axis is Age and the x-axis is Survived.
Also, if you summarize it, there are lots of NA’s. So, let’s exclude the variable Age because it doesn’t have a big impact on Survived and because the NA's make it hard to work with.
summary(train$Age)
Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
0.42 20.12 28.00 29.70 38.00 80.00 177 In the below boxplot, the boxplot for Fares are much different for those who survived and those who didn’t. Again, the y-axis is Fare and the x-axis is Survived.
bplot.xy(train$Survived, train$Fare)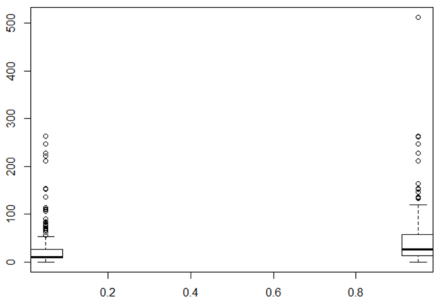 Box Plot For Fair – Random Forest In R
Box Plot For Fair – Random Forest In R
Summarizing, you’ll find that there are no NA’s for Fare. So, let’s include this variable.
summary(train$Fare)
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.00 7.91 14.45 32.20 31.00 512.33 The next step is to convert Survived to a Factor data type so that caret builds a classification instead of a regression model. After that, we use a simple train command to train the model.
Now the model is trained using the random forest algorithm that we discussed earlier. Random forest is perfect for such problems because it performs numerous computations and predicts the results with high accuracy.
train$Survived <- factor(train$Survived)
# Set a random seed
set.seed(51)
# Training using ‘random forest’ algorithm
model <- train(Survived ~ Pclass + Sex + SibSp +
Embarked + Parch + Fare, # Survived is a function of the variables we decided to include
data = train, # Use the train data frame as the training data
method = 'rf',# Use the 'random forest' algorithm
trControl = trainControl(method = 'cv', # Use cross-validation
number = 5) # Use 5 folds for cross-validationTo evaluate our model, we will use cross-validation scores.
Cross-validation is used to assess the efficiency of a model by using the training data. You start by randomly dividing the training data into 5 equally sized parts called “folds”. Next, you train the model on 4/5 of the data and check its accuracy on the 1/5 of the data you left out. You then repeat this process with each split of the data.
In the end, you average the percentage accuracy across the five different splits of the data to get an average accuracy. Caret does this for you, and you can see the scores by looking at the model output:
model
Random Forest
891 samples
6 predictor
2 classes: '0', '1'
No pre-processing
Resampling: Cross-Validated (5 fold)
Summary of sample sizes: 712, 713, 713, 712, 714
Resampling results across tuning parameters:
mtry Accuracy Kappa
2 0.8047116 0.5640887
5 0.8070094 0.5818153
8 0.8002236 0.5704306
Accuracy was used to select the optimal model using the largest value.
The final value used for the model was mtry = 5.The first thing to notice is where it says, “The final value used for the model was mtry = 5.” The “mtry” is a hyper-parameter of the random forest model that determines how many variables the model uses to split the trees.
The table shows different values of mtry along with their corresponding average accuracy under cross-validation. Caret automatically picks the value of the hyper-parameter “mtry” that is the most accurate under cross-validation.
In the output, with mtry = 5, the average accuracy is 0.8170964, or about 82 percent, which is the highest value, hence Caret picks this value for us.
Before we predict the output for the test data, let’s check if there is any missing data in the variables we are using to predict. If Caret finds any missing values, it will not return a prediction at all. So, we must find the missing data before moving ahead:
summary(test)Notice the variable “Fare” has one NA value. Let’s fill in that value with the mean of the “Fare” column. We use an if-else statement to do this.
So, if an entry in the column “Fare” is NA, then replace it with the mean of the column and remove the NA’s when you take the mean:
test$Fare <- ifelse(is.na(test$Fare), mean(test$Fare, na.rm = TRUE), test$Fare)Now, our final step is to make predictions on the test set. To do this, you just have to call the predict method on the model object you trained. Let’s make the predictions on the test set and add them as a new column.
test$Survived <- predict(model, newdata = test)
test$Survived
Here you can see the “Survived” values (either 0 or 1) for each passenger. Where one stands for survived and 0 stands for died. This prediction is made based on the “pclass” and “Fare” variables. You can use other variables too, if they are somehow related to whether a person boarding the titanic will survive or not.
I hope you all found this blog informative. If you have any thoughts to share, please comment.
Further Reading
Published at DZone with permission of Zulaikha Geer, DZone MVB. See the original article here.
Opinions expressed by DZone contributors are their own.

Comments